こんにちは。だいCです。
以前 運動知能研ライブラリ milib の環境構築をしてみました。
今回からライブラリの中身を見ていきたいと思います。
まず最初にmilibの計算の根幹となる「ZEDA」について見ていきたいと思います。
1. milib構成におけるZEDAの位置づけ
Z-Labの公開ソフトウェアのページを見ると、milibの構成は以下のようになっているそうです。
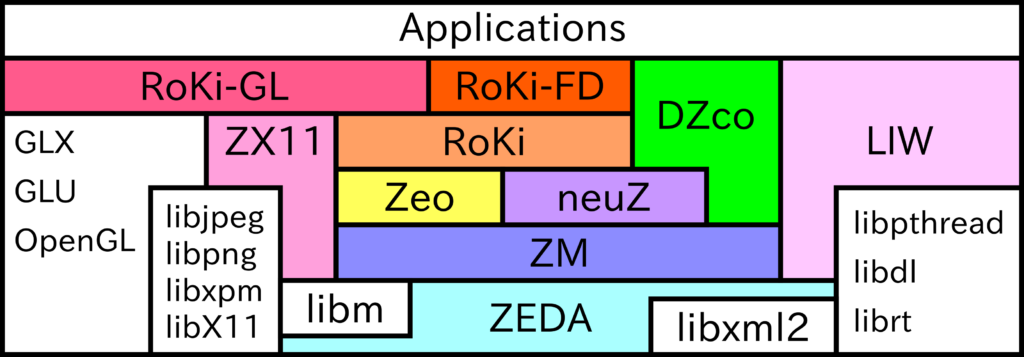
OS上で動作することを考えると、以下のようなイメージだと思っています。
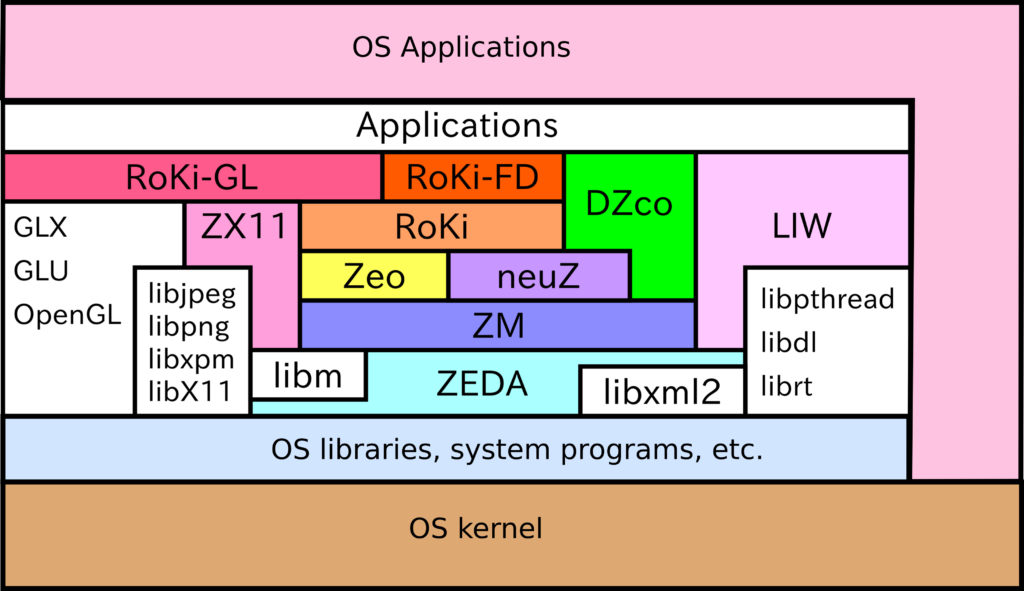
OSを構成する標準ライブラリやOSをCPU上で動作させるカーネルがmilibの実行環境を支えているイメージです。
milibの対応OSは、milibが依存している標準ライブラリが使用できればどこでも良いかと思います。
milibはユーザランドで動作し、標準ライブラリからOSカーネルのI/Oシステムコールを叩き外部デバイスと連携し現実の物理世界へとアクセスするイメージかと思います。
milibを使用するユーザアプリケーション(図中階層一番上の「Applications」)から見ると、そのように現実の物理世界へアクセスすることもできますし、Roki系ライブラリを駆使してシミュレータを構築し仮想上の物理世界へアクセスすることもできるのかな、と思います。
一番下の階層にいるのがZEDAですね。
ZEDAとは Z Elementary Data Algorithm の略だそうです。milib共通のデータ要素アルゴリズムを構築しているようです。
2. ZEDAパッケージのディレクトリ構成
まずはソースコードのパッケージからZEDAライブラリの構成をざっくり見てみましょう。
以前「milib環境を構築してみよう」でクローンされた環境をそのまま見てみます。
自動でクローンされたmilibパッケージのディレクトリ構成は以下のようになっていました。
milib/
├── bin/
├── include/
├── lib/
└── milib-starter/
├── README.md
├── config
├── deb/
├── dzco/
├── liw/
├── neuz/
├── roki/
├── roki-fd/
├── roki-gl/
├── scripts/
├── zeda/ <-- Here
├── zeo/
├── zm/
└── zx11/「Here」と書いた場所に zeda のソースコードパッケージが配置されています。
milib-starter の中に格納されていたのでした。
zeda/の中身を見てみましょう。{YOUR_DIR} はmilibを配置した自分の好きなディレクトリを指しています。
# 現在zedaディレクトリにいることを確認
$ pwd
{YOUR_DIR}/milib/milib-starter/zedatree コマンド等で見ると以下のようなディレクトリ構成になっているようです。
zeda/
├── COPYING
├── GPL-3
├── HISTORY
├── LGPL-3
├── README.ZTK.md
├── README.md
├── config
├── config.org
├── makefile
├── app/
├── doc/
├── example/
├── include/
├── lib/
├── src/
├── test/
└── tools/
README.md がありますね。
3. ZEDAのREADME
まずは ZEDA の REAMDE.md を読んでみましょう。
以下、自分の言葉で勝手に日本語に訳してみました。
~~~
ZEDA – Elementary Data and Algorithms
Copyright (C) Tomomichi Sugihara (Zhidao) since 1998
[なんですか?これ]
ZEDA頻繁に使用されるデータ構造とアルゴリズムの以下を含むコレクションだよ:
- ビット演算
- 配列型演算
- リスト型演算
- ツリー型演算
- ラウンド-ロビン テーブル
- 文字列型演算
- コマンドライン オプション操作
- 一般的な I/O ストリーム
- 乱数生成器
- ZTK フォーマット パーサー
- CSV ファイル操作
- XML パーサー(libxml2のラッパー)
[インストール / アンインストール方法]
インストール
ZEDAをインストールしたいディレクトリへ移動し、以下を実行してね:
% git clone https://github.com/zhidao/zeda.git
% cd zedaヘッダファイル、ライブラリ、ユーティリティを特定のディレクトリにするために、もし必要ならば config ファイルの中の PREFIX を編集してインストールしてね。 (デフォルトのインストール場所: ~/usr)
- ヘッダファイル: $PREFIX/include/zeda
- ライブラリファイル: $PREFIX/lib
- ユーティリティ: $PREFIX/bin
それから, make して install してね。
% make && make installアンインストール
以下を実行してね:
% make uninstallこれにより $PREFIX/lib/libzeda.so と $PREFIX/include/zeda が削除されるよ。
[つかいかた]
自分の環境変数 PATH と LD_LIBRARY_PATH を設定しておいてね。これは以下を実行するよ:
% export PATH=$PATH:$PREFIX/bin
% export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:$PREFIX/libBourne shell ファミリー (bash, zsh, etc.) 、または
C shell ファミリー (csh, tcsh, etc.)なら以下のように設定するよ:
% set path = ( $path $PREFIX/bin )
% setenv LD_LIBRARY_PATH $LD_LIBRARY_PATH:$PREFIX/lib自分の test.c コードをコンパイルしたいときは、例えば、対のような行で動作するよ。
% gcc `zeda-config -L` `zeda-config -I` test.c `zeda-config -l`[ドキュメント]
http://www.doxygen.org/ から doxygen をダウンロードして以下を実行してね:
% make documentHTMLドキュメントが doc/ 以下に生成されるよ。
[お問い合わせ]
~~~
ふむふむ。
インストールは既に「milib環境を構築してみよう」で実施されているのでスキップしますね。
ドキュメントがあるとのことです。
4. コピーライト/ライセンス
zeda/ ディレクトリ内の COPYING を見ると、ZEDAはフリーソフトウェアであり、コピーライトは Tomomichi Sugihara 氏、使用許諾は一部 GPL、LGPLライセンスに基づいているようです。ライセンスによっては複製・改変・使用したもの(派生物含む)を公開・頒布する場合ソースコードの開示義務があるので、オープンソースソフトウェアを商用利用する方はよく注意しておきましょう。
5. 環境パスを通しておく
とりあえず、README.md の [つかいかた] に従い、環境パスを通しておきます。
milib/ ディレクトリに置いてある config ファイルの設定を反映しておき、パスを通しておきます。
$ pwd # milibディレクトリに居ることを確認。
{YOUR_DIR}/milib
$ . ./config # configファイル内の設定を現在の端末に反映。
$ echo $PREFIX # 変数PREFIXが反映されていることを確認
{YOUR_DIR}/milib
# 環境パスを通す
$ export PATH=$PATH:$PREFIX/bin
$ export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:$PREFIX/lib
6. ZEDAのdoxygenドキュメント出力
README.mdに書いてあるように、doxygen 形式のドキュメントを出力できるようです。
doxygenをインストールしておきます。
$ sudo apt install doxygen上記インストールで GraphViz という、関数の呼び出し関係のグラフや UML 図を自動生成してくれるライブラリもインストールしてくれるようです。
README.mdにあるように、make document を実行してドキュメントを doc/ へ出力してみます。
$ pwd # zeda/に居ることを確認
{YOUR_DIR}/milib/milib-starter/zeda
$ make document
make: *** ターゲット 'document' を make するルールがありません. 中止.出力できませんでした。
zeda/makefile のルールに document を指定したものは無いようです。
zeda/makefile の中身を見てみると、以下のようなドキュメント出力っぽい記述がありました。
doc: @$(MAKEFILEGEN) | make -f - doc
今度は make doc を実行してみます。
$ make doc
make: 'doc' は更新済みです.はて?
どうやら zeda/ 下で make doc では更新済みとみなされているようです。zeda/makefile を読むと zeda-makefile-gen というスクリプトを実行していて、本スクリプトのヘルプを見てみると( $ zeda-makefile-gen をそのまま実行)、 zeda/doc/ の中で make を実行するようです。しかし失敗していたので、手動で zeda/doc/ 下で make を実行してみました。
$ pwd # zeda/doc/ に居ることを確認
{YOUR_DIR}/milib/milib-starter/zeda/doc
$ make
warning: Tag `USE_WINDOWS_ENCODING' at line 14 of file `-' has become obsolete.
To avoid this warning please remove this line from your configuration file or upgrade it using "doxygen -u"
warning: Tag `DETAILS_AT_TOP' at line 30 of file `-' has become obsolete.
To avoid this warning please remove this line from your configuration file or upgrade it using "doxygen -u"
warning: Tag `SHOW_DIRECTORIES' at line 98 of file `-' has become obsolete.
To avoid this warning please remove this line from your configuration file or upgrade it using "doxygen -u"
warning: Tag `HTML_ALIGN_MEMBERS' at line 171 of file `-' has become obsolete.
To avoid this warning please remove this line from your configuration file or upgrade it using "doxygen -u"
--- (後略) ---warning がいくつか出ていますが、今度はどうやらドキュメント出力に成功したようです。
doc/ 下に以下のような html/ 、 man/ 、 tex/ といった成果物が出力されていました。
zeda/
└── doc/
├── dox.conf
├── makefile
├── html/
├── man/
└── tex/
7. ZEDAドキュメント
出力された ZEDAライブラリのdoxygen形式の html/ ドキュメントを以下に上げておきます。
7.1. ZEDAのインクルード依存関係
ZEDAのdoxygenドキュメント出力からファイル構成を視覚的に見ることができます。
zeda.h というヘッダファイルの依存関係グラフを見ると、このファイルがZEDAライブラリをインクルードするための親玉的な存在であることが分かります。
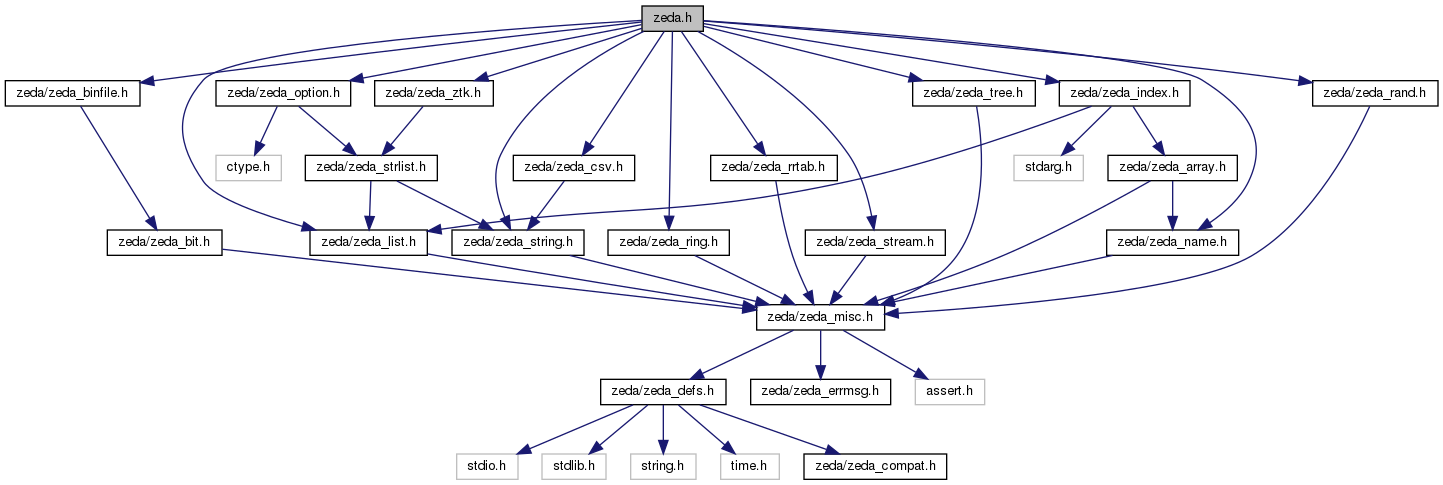
7.2. ZEDAライブラリの依存関係
以前 milib のインストールを実行した際に、ソースコードがコンパイルされ、ZEDAライブラリが既に出力されています。
ZEDAパッケージの中の lib/ の中に libzeda.so という共有ライブラリがあると思います。
zeda/
└── lib/
└── libzeda.soldd コマンドでこの共有ライブラリの依存関係を見ておきましょう。
$ ldd libzeda.so
linux-vdso.so.1
libc.so.6 => /lib/x86_64-linux-gnu/libc.so.6
/lib64/ld-linux-x86-64.so.2上の表示では、各ライブラリのメモリへロードされる時のアドレス表記は省略しています。
依存関係より、Linuxの仮想動的共有オブジェクトのライブラリ、cライブラリ、リンカライブラリという、Linux上でC言語由来の共有ライブラリを動作させるための最低限の構成で成り立っていることが分かります。
8. 例 zListClass を読んでみる
ここから少しだけ ZEDAライブラリ のソースコードを味見してみましょう。
例として、配列型演算などもありますがC標準ライブラリでもよく見るようなデータ型は簡単なので、ZEDAのリスト型データ zListClass の定義を見てみます。C++ の STL(Standard Template Library)コンテナで見たことがある人は読みやすいかもしれません。
これは、 zeda_list.h にほぼ定義が書かれています。
ZEDAでは、双方向循環型のリストをデータ型 zListClass として定義してあるようです。
このリスト型のイメージを以下のように描いてみました。
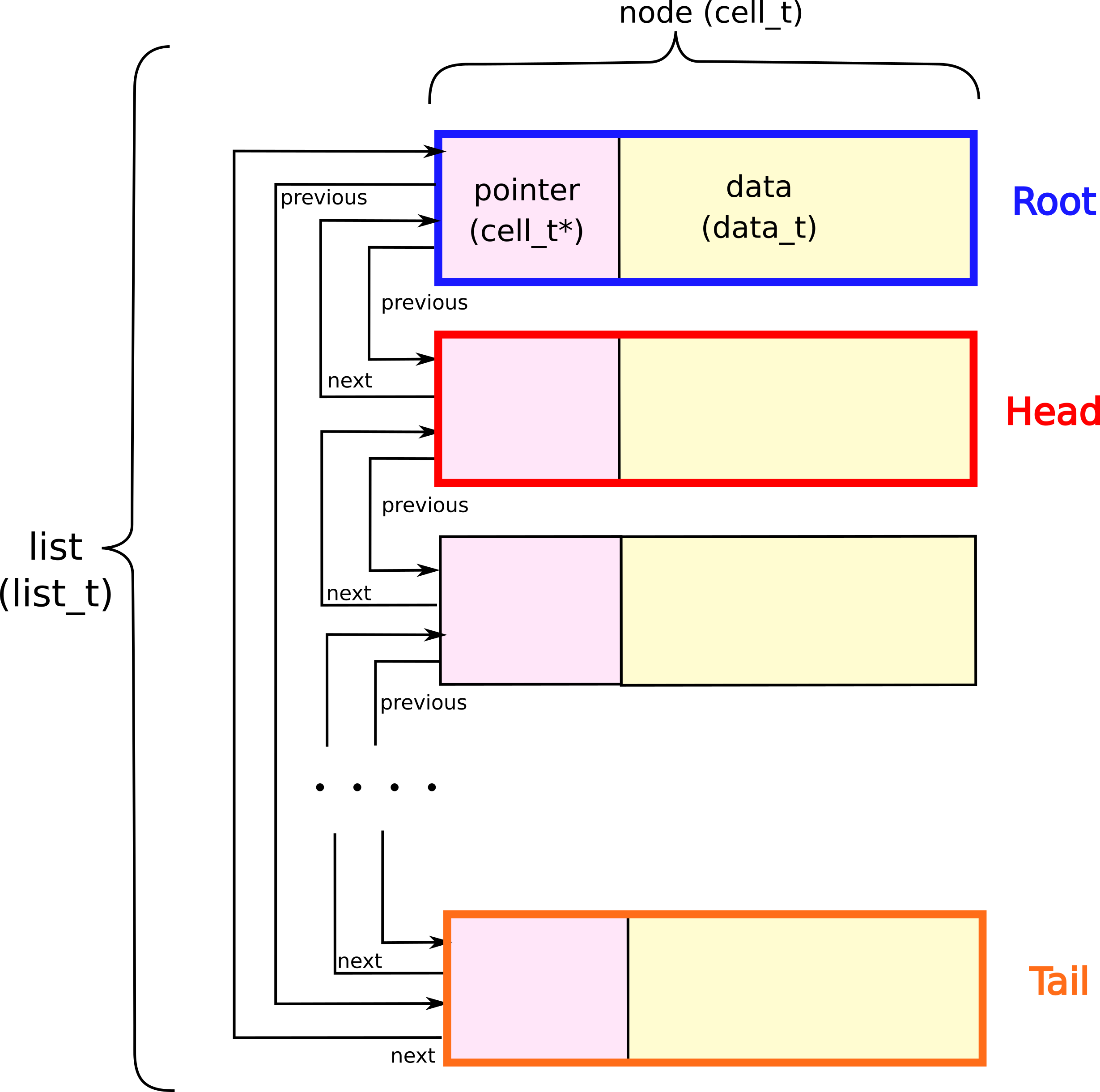
リスト型は複数データを隣同士でつないで簡単に格納/削除できるようにしたものだそうです。
ZEDAでは要素単位はポインタとデータを持ったノードとして定義されます。
ノードは隣のノードの場所を示すポインタを持っています。zListClass では両隣の双方向のポインタを持たせてあり、図のようにリング状に連なっているようです。隣のポインタはそれぞれprevとnextとして示されています。
zListClass の定義を見てみましょう。
#define zListClass(list_t,cell_t,data_t) \
typedef struct __##cell_t{\
struct __##cell_t *prev, *next;\
data_t data;\
} cell_t;\
typedef struct __##list_t{\
int size;\
cell_t root;\
} list_tマクロ関数を使用して構造体定義を内包しクラスっぽく定義しています。
list_t はリスト型の定義名で自由に定義できます。
cell_t はノード型の定義名で自由に定義できます。
data_tはデータ型の定義名でintやcharや自分でtypedefして作成したオリジナルのデータ型など自由に入れられます。
見て分かるようにC++のクラスとは異なりコンストラクタやデストラクタはありません。
格納したデータのメモリ解放はクラスオブジェクト生成したあと別途明示的に書く必要があります。
そのため zListDestroy() というマクロ関数が別途解放処理のために定義されてあります。
では zeda_list.h を使用してリスト型データ zListClass をためしてみましょう。
以下、zeda/example/list/ 内のサンプルコードを参考にして、Double型の値をお尻に次々に追加して双方向循環型リスト作成するサンプルを書いてみました。
#include <zeda/zeda_list.h>
int main(void)
{
/* double型リストの定義 */
zListClass( DoubleList, DoubleListCell, double);
DoubleList dl1;
/* 1つ目のノードを作成 */
DoubleListCell dc1;
dc1.data = 1.0;
/* 1つ目のノードを初期化してルートとしてリストに格納 */
zListCellInit( &dc1 );
dl1.root = dc1;
zListInit( &dl1 );
/* 以下同様にノードを作成しリストのお尻に格納していく */
DoubleListCell dc2;
dc2.data = 2.0;
zListInsertTail( &dl1, &dc2 );
DoubleListCell dc3;
dc3.data = 3.0;
zListInsertTail( &dl1, &dc3 );
/* リストの中身を表示 */
DoubleListCell *dcp;
zListForEach( &dl1, dcp )
printf( "value = %lf\n", dcp->data );
/* Headノードの確認 */
printf( "value of Head node = %lf\n", zListHead( &dl1 )->data );
/* Tailノードの確認 */
printf( "value of Tail node = %lf\n", zListTail( &dl1 )->data );
/* 最初から順にノード確認 */
dcp = zListRoot( &dl1 );
printf( "1st is Root = %lf\n", dcp->data );
dcp = zListCellPrev( dcp );
printf( "2nd previous from Root = %lf\n", dcp->data );
dcp = zListCellPrev( dcp );
printf( "3rd previous from Root = %lf\n", dcp->data );
dcp = zListCellPrev( dcp );
printf( "4th previous from Root = %lf\n", dcp->data );
return 0;
}このサンプルをコンパイルするときの makefile は以下になります。
前述のとおり端末に環境パスが通っていることが前提となります。
INCLUDE=`zeda-config -I`
LIB=`zeda-config -L`
LINK=`zeda-config -l`
CC=gcc
CFLAGS=-ansi -Wall -O3 $(LIB) $(INCLUDE) -funroll-loops
all : zeda_list_sample
% : %.c
$(CC) $(CFLAGS) -o $@ $< $(LINK)
clean :
-@rm -f *.o *~ coreこれら zeda_list_sample.c と makefile を同じ場所において以下 make を実行します。
$ makezeda_list_sample という実行ファイルが生成されたと思います。
リストがうまく生成できたか実行してみます。
$ ./zeda_list_sample
value = 3.000000
value = 2.000000
value of Head node = 2.000000
value of Tail node = 3.000000
1st is Root = 1.000000
2nd previous from Root = 2.000000
3rd previous from Root = 3.000000
4th previous from Root = 1.000000zListForEach() は最後に格納したお尻から頭へと順にたどっていくようです。ルートは含まないようです。
格納したdoubleのデータ値をもったリストが無事作成できているようです。
9. 今回はここまで。
ふぅ〜。
milibチャレンジ第一回としてZEDAライブラリについて見てみました。
ZEDAは他にもツリー構造やI/Oストリームなど興味深いデータ定義が実装されているようです。
C++だと何だそんなの簡単そうと浅く思えるものも、Cでプリプロセッサやポインタのテクニックを駆使して実現するのはプログラムのアイデアとして非常に奥深く勉強になります。
中でもZTKフォーマットに関する機能はのちのち重要になってきそうです。
ZTKとは何でしょう?という所も含めて次回以降見ていきたいです。
では。