こんにちは。だいCです。

このブログはノート代わりに使わせてもらっています。

前回、回転運動の速度をどのように表すかで、回転行列の速度\( \dot {\bf R}(t) \)を求めました。

「速度が求まってので、次は加速度いってみよー！！」と言いたいところですが、

その前にこの回転行列の速度\( \dot {\bf R}(t) \)が、何なのかをもう少し考えたいと思います。

目的

回転行列の速度\( \dot {\bf R}(t) \)が何かを示す。

回転行列\( \bf R \)の意味

まずそもそも、回転行列\( {\bf R}(t) \)とは、何なのかを考えます。

プログラムとして見ると、\( {\bf R}(t) \)は時刻\( t \)を入力にして行列を返す関数に見えますが、

もう少し内部仕様を掘ってみると、回転行列\( {\bf R } \)の直接の入力は、時刻\( t \)でなく回転角\( \theta \)です。

時刻\( t \)は、回転角を返す関数\( \theta(t) \)の入力です。

この関数\( \theta(t) \)は、内部で軌道計算をします。入出力は以下のようになります。

回転角の関数\( \theta(t) \)

• 入力：時刻\( t \)
• 出力：その時刻\( t \)での角度\( \theta \)

回転行列\( {\bf R } \)は、\( {\bf R }(\theta) \)として、以下のように書けます。

回転行列の関数\( {\bf R }(\theta) \)

• 入力：時刻\( t \)での角度\( \theta \)
• 出力：その角度\( \theta \)での行列

では、この出力の行列は何を表しているのかを考えます。

回転行列の性質は

広瀬茂男先生の「ロボット工学 ー機械システムのベクトル解析ー」、

川崎晴久先生の教科書「ロボット工学の基礎」、

梶田秀司先生の教科書「ヒューマノイドロボット」を読むと分かりやすいです。

絶対座標系の基底を直交単位ベクトル(いわゆるx軸, y軸, z軸方向の単位ベクトル)を \( {}^{0}{\bf e}_{x} \), \( {}^{0}{\bf e}_{y}\), \( {}^{0}{\bf e}_{z}\)とします。それぞれの座標値は以下のようなります。

$$  \begin{array}{rcl}
{}^{0}{\bf e}_{x} = \left[ \begin{array}{c}
1 \\
0 \\
0
\end{array} \right]
,\ \ \ &
{}^{0}{\bf e}_{y} = \left[ \begin{array}{c}
0 \\
1 \\
0
\end{array} \right]
,\ \ \ &
{}^{0}{\bf e}_{z} = \left[ \begin{array}{c}
0 \\
0 \\
1
\end{array} \right]
\end{array} $$

ここで絶対座標系と書きましたが、絶対座標系とは、、

• 座標系のボス的存在で、
• すべての座標の基準となる座標系、
• 空間上の点の座標を数多くの座標系間基準で相対的に表現しまくるのに対し、唯一絶対的な座標表現をするときの基準となる座標系、
• 相対座標系の対称として表顕される座標系

座標系については、別ページにまとめておきます。

今は基準座標系の話をしたいわけではありませんが、

座標表現されたベクトルの座標は必ず、基準座標系が何であるかを把握した上で使用しなければいけません。

特に３Dビジョンや双腕マニピュレータ、移動ロボット等で座標系をバンバン切り替えて操作するときは、間違えると危険です。

１つの絶対座標系を基準に表現しておくと、ややこしい座標系間の相対関係を考えるとき分かりやすくなります。

それでは話を戻して、

絶対座標系の基底を直交単位ベクトル(いわゆるx軸, y軸, z軸方向の単位ベクトル) を\( {\bf e}_{x} \), \( {\bf e}_{y}\), \( {\bf e}_{z}\)としました。

単位ベクトル、つまり大きさが１で、互いに直交する基底(互いに独立)なので、このベクトルを「正規直交基底」と言ったりするそうです。

３次元のベクトル空間は、基準となる座標系の３本の基底ベクトルで表現されます。線形代数の授業ですね。懐かしい。

以降、左上に基準座標系のラベルを書きます。

右下にその基準座標で表された注目する変数のラベルを書きます。

たとえば、あるベクトル\({\bf p} \)は、
座標系\( \Sigma_{A} \)基準の基底ベクトル\( {}^{A}{\bf e}_{x} \), \( {}^{A}{\bf e}_{y} \), \( {}^{A}{\bf e}_{z} \)により、\({}^{A}{\bf p} \)として表現すると、以下のように書きます。

$$ \begin{array}{rcl}
{}^{A}{\bf p} &=&
\left[ \begin{array}{ccc} {}^{A}p_x & {}^{A}p_y & {}^{A}p_z \end{array} \right]^{\rm T} \\
&=&
{}^{A}p_{x}{}^{A}{\bf e}_{x} +
{}^{A}p_{y}{}^{A}{\bf e}_{y} +
{}^{A}p_{z}{}^{A}{\bf e}_{z}
\end{array}
$$

ここで、\( {}^{A}{\bf e}_{x} \), \( {}^{A}{\bf e}_{y}\), \( {}^{A}{\bf e}_{z}\)それぞれの座標は以下のようなります。

$$  \begin{array}{rcl}
{}^{A}{\bf e}_{x} = \left[ \begin{array}{c}
1 \\
0 \\
0
\end{array} \right]
,\ \ \ &
{}^{A}{\bf e}_{y} = \left[ \begin{array}{c}
0 \\
1 \\
0
\end{array} \right]
,\ \ \ &
{}^{A}{\bf e}_{z} = \left[ \begin{array}{c}
0 \\
0 \\
1
\end{array} \right]
\end{array} $$

同様に、このベクトル\({\bf p} \)は

絶対座標系\( \Sigma_{0} \)基準の基底ベクトル\( {}^{0}{\bf e}_{x} \), \( {}^{0}{\bf e}_{y} \), \( {}^{0}{\bf e}_{z} \)により、\({}^{0}{\bf p}\)として表現すると、以下のように書けます。

$$ \begin{array}{rcl}
{}^{0}{\bf p} &=&
\left[ \begin{array}{ccc} {}^{0}p_x & {}^{0}p_y & {}^{0}p_z \end{array} \right]^{\rm T} \\
&=&
{}^{0}p_{x}{}^{0}{\bf e}_{x}
+ {}^{0}p_{y}{}^{0}{\bf e}_{y}
+ {}^{0}p_{z}{}^{0}{\bf e}_{z}
\end{array}
$$

では、座標系の変換を考えたいと思います。

いま、座標系\( \Sigma_{A} \)基準の基底ベクトル\( {}^{A}{\bf e}_{x} \), \( {}^{A}{\bf e}_{y} \), \( {}^{A}{\bf e}_{z} \)を、絶対座標系\( \Sigma_{0} \)基準で見たとき以下のように\( {}^{0}{\bf x}_{{}^{A}{\bf e}_{x}} \), \( {}^{0}{\bf y}_{{}^{A}{\bf e}_{y}} \), \( {}^{0}{\bf z}_{{}^{A}{\bf e}_{x}} \)と表せるとします。

$$ \begin{array}{rcl}
{}^{A}{\bf e}_{x}
& {}^{\Sigma_{A}}\longrightarrow^{\Sigma_{0}} &\ \
{}^{0}{\bf x}_{{}^{A}{\bf e}_{x}} =
\left[ \begin{array}{c}
{}^{0}x_{{}^{A}{\bf e}_{x}x} \\
{}^{0}x_{{}^{A}{\bf e}_{x}y} \\
{}^{0}x_{{}^{A}{\bf e}_{x}z}
\end{array} \right], \\
{}^{A}{\bf e}_{y}
& {}^{\Sigma_{A}}\longrightarrow^{\Sigma_{0}} &\ \
{}^{0}{\bf y}_{{}^{A}{\bf e}_{y}} =
\left[ \begin{array}{c}
{}^{0}y_{{}^{A}{\bf e}_{y}x} \\
{}^{0}y_{{}^{A}{\bf e}_{y}y} \\
{}^{0}y_{{}^{A}{\bf e}_{y}z}
\end{array} \right], \\
{}^{A}{\bf e}_{z}
& {}^{\Sigma_{A}}\longrightarrow^{\Sigma_{0}} &\ \
{}^{0}{\bf z}_{{}^{A}{\bf e}_{z}} =
\left[ \begin{array}{c}
{}^{0}z_{{}^{A}{\bf e}_{z}x} \\
{}^{0}z_{{}^{A}{\bf e}_{z}y} \\
{}^{0}z_{{}^{A}{\bf e}_{z}z}
\end{array} \right],
\end{array}
$$

この変換の関係を使用して、

上記の\( {}^{0}{\bf p} \)を、かなり無理矢理ですが、以下のように式変形します。

特に二段目から三段目、五段目から六段目の式変形は、ふつう導出では出てこない、かなり無理矢理な便宜上の変形です。

$$ \begin{array}{rcl}
{}^{0}{\bf p} &=&
\left[ \begin{array}{ccc} {}^{0}p_x & {}^{0}p_y & {}^{0}p_z \end{array} \right]^{\rm T} \\
&=&
{}^{0}p_{x}{}^{0}{\bf e}_{x}
+ {}^{0}p_{y}{}^{0}{\bf e}_{y}
+ {}^{0}p_{z}{}^{0}{\bf e}_{z}\\
&=&
{}^{A}p_{x}
\left( {}^{0}x_{{}^{A}{\bf e}_{x}x}{}^{0}{\bf e}_{x}
+  {}^{0}x_{{}^{A}{\bf e}_{x}y}{}^{0}{\bf e}_{y}
+ {}^{0}x_{{}^{A}{\bf e}_{x}z}{}^{0}{\bf e}_{z}\right)  \\
&\ &\ +
{}^{A}p_{y}
\left( {}^{0}y_{{}^{A}{\bf e}_{y}x}{}^{0}{\bf e}_{x}
+  {}^{0}y_{{}^{A}{\bf e}_{y}y}{}^{0}{\bf e}_{y}
+ {}^{0}y_{{}^{A}{\bf e}_{y}z}{}^{0}{\bf e}_{z}
\right) \\
&\ &\ +
{}^{A}p_{z}
\left( {}^{0}z_{{}^{A}{\bf e}_{z}x}{}^{0}{\bf e}_{x}
+  {}^{0}z_{{}^{A}{\bf e}_{z}y}{}^{0}{\bf e}_{y}
+ {}^{0}z_{{}^{A}{\bf e}_{z}z}{}^{0}{\bf e}_{z}
\right) \\
&=&
{}^{A}p_{x}
\left[ \begin{array}{c}
{}^{0}x_{{}^{A}{\bf e}_{x}x} \\
{}^{0}x_{{}^{A}{\bf e}_{x}y} \\
{}^{0}x_{{}^{A}{\bf e}_{x}z}
\end{array} \right] +
{}^{A}p_{y}
\left[ \begin{array}{c}
{}^{0}y_{{}^{A}{\bf e}_{y}x} \\
{}^{0}y_{{}^{A}{\bf e}_{y}y} \\
{}^{0}y_{{}^{A}{\bf e}_{y}z}
\end{array} \right] +
{}^{A}p_{z}
\left[ \begin{array}{c}
{}^{0}z_{{}^{A}{\bf e}_{z}x} \\
{}^{0}z_{{}^{A}{\bf e}_{z}y} \\
{}^{0}z_{{}^{A}{\bf e}_{z}z}
\end{array} \right] \\
&=&
{}^{A}p_{x}{}^{0}{\bf x}_{{}^{A}{\bf e}_{x}} +
{}^{A}p_{y}{}^{0}{\bf y}_{{}^{A}{\bf e}_{y}} +
{}^{A}p_{z}{}^{0}{\bf z}_{{}^{A}{\bf e}_{z}} \\
&=&
{}^{A}p_{x} \left[
\left[ \begin{array}{ccc}
{}^{0}x_{{}^{A}{\bf e}_{x}x} &
{}^{0}y_{{}^{A}{\bf e}_{y}x} &
{}^{0}z_{{}^{A}{\bf e}_{z}x}
\end{array} \right]
\left[ \begin{array}{c}
1 \\
0 \\
0
\end{array} \right] \right. \\
&\ &\ \ \ \ \ \ \ \ \ ,
\left.
\left[ \begin{array}{ccc}
{}^{0}x_{{}^{A}{\bf e}_{x}y} &
{}^{0}y_{{}^{A}{\bf e}_{y}y} &
{}^{0}z_{{}^{A}{\bf e}_{z}y}
\end{array} \right]
\left[ \begin{array}{c}
1 \\
0 \\
0
\end{array} \right]
\right. \\
&\ &\ \ \ \ \ \ \ \ \ ,
\left.
\left[ \begin{array}{ccc}
{}^{0}x_{{}^{A}{\bf e}_{x}z} &
{}^{0}y_{{}^{A}{\bf e}_{y}z} &
{}^{0}z_{{}^{A}{\bf e}_{z}z}
\end{array} \right]
\left[ \begin{array}{c}
1 \\
0 \\
0
\end{array} \right]
\right]
\\
&\ & +
{}^{A}p_{y} \left[
\left[ \begin{array}{ccc}
{}^{0}x_{{}^{A}{\bf e}_{x}x} &
{}^{0}y_{{}^{A}{\bf e}_{y}x} &
{}^{0}z_{{}^{A}{\bf e}_{z}x}
\end{array} \right]
\left[ \begin{array}{c}
0 \\
1 \\
0
\end{array} \right] \right. \\
&\ &\ \ \ \ \ \ \ \ \ ,
\left.
\left[ \begin{array}{ccc}
{}^{0}x_{{}^{A}{\bf e}_{x}y} &
{}^{0}y_{{}^{A}{\bf e}_{y}y} &
{}^{0}z_{{}^{A}{\bf e}_{z}y}
\end{array} \right]
\left[ \begin{array}{c}
0 \\
1 \\
0
\end{array} \right]
\right. \\
&\ &\ \ \ \ \ \ \ \ \ ,
\left.
\left[ \begin{array}{ccc}
{}^{0}x_{{}^{A}{\bf e}_{x}z} &
{}^{0}y_{{}^{A}{\bf e}_{y}z} &
{}^{0}z_{{}^{A}{\bf e}_{z}z}
\end{array} \right]
\left[ \begin{array}{c}
0 \\
1 \\
0
\end{array} \right]
\right] \\
&\ & +
{}^{A}p_{z} \left[
\left[ \begin{array}{ccc}
{}^{0}x_{{}^{A}{\bf e}_{x}x} &
{}^{0}y_{{}^{A}{\bf e}_{y}x} &
{}^{0}z_{{}^{A}{\bf e}_{z}x}
\end{array} \right]
\left[ \begin{array}{c}
0 \\
0 \\
1
\end{array} \right] \right. \\
&\ &\ \ \ \ \ \ \ \ \ ,
\left.
\left[ \begin{array}{ccc}
{}^{0}x_{{}^{A}{\bf e}_{x}y} &
{}^{0}y_{{}^{A}{\bf e}_{y}y} &
{}^{0}z_{{}^{A}{\bf e}_{z}y}
\end{array} \right]
\left[ \begin{array}{c}
0 \\
0 \\
1
\end{array} \right]
\right. \\
&\ &\ \ \ \ \ \ \ \ \ ,
\left.
\left[ \begin{array}{ccc}
{}^{0}x_{{}^{A}{\bf e}_{x}z} &
{}^{0}y_{{}^{A}{\bf e}_{y}z} &
{}^{0}z_{{}^{A}{\bf e}_{z}z}
\end{array} \right]
\left[ \begin{array}{c}
0 \\
0 \\
1
\end{array} \right]
\right] \\
&=&
{}^{A}p_{x}
\left[ \begin{array}{ccc}
{}^{0}x_{{}^{A}{\bf e}_{x}x}  & {}^{0}y_{{}^{A}{\bf e}_{y}x}   & {}^{0}z_{{}^{A}{\bf e}_{z}x}  \\
{}^{0}x_{{}^{A}{\bf e}_{x}y}  & {}^{0}y_{{}^{A}{\bf e}_{y}y}   & {}^{0}z_{{}^{A}{\bf e}_{z}y}  \\
{}^{0}x_{{}^{A}{\bf e}_{x}z}  & {}^{0}y_{{}^{A}{\bf e}_{y}z}   & {}^{0}z_{{}^{A}{\bf e}_{z}z}
\end{array} \right]
\left[ \begin{array}{c}
1 \\
0 \\
0
\end{array} \right] \\
&\ & +
{}^{A}p_{y}
\left[ \begin{array}{ccc}
{}^{0}x_{{}^{A}{\bf e}_{x}x}  & {}^{0}y_{{}^{A}{\bf e}_{y}x}   & {}^{0}z_{{}^{A}{\bf e}_{z}x}  \\
{}^{0}x_{{}^{A}{\bf e}_{x}y}  & {}^{0}y_{{}^{A}{\bf e}_{y}y}   & {}^{0}z_{{}^{A}{\bf e}_{z}y}  \\
{}^{0}x_{{}^{A}{\bf e}_{x}z}  & {}^{0}y_{{}^{A}{\bf e}_{y}z}   & {}^{0}z_{{}^{A}{\bf e}_{z}z}
\end{array} \right]
\left[ \begin{array}{c}
0 \\
1 \\
0
\end{array} \right] \\
&\ & +
{}^{A}p_{z}
\left[ \begin{array}{ccc}
{}^{0}x_{{}^{A}{\bf e}_{x}x}  & {}^{0}y_{{}^{A}{\bf e}_{y}x}   & {}^{0}z_{{}^{A}{\bf e}_{z}x}  \\
{}^{0}x_{{}^{A}{\bf e}_{x}y}  & {}^{0}y_{{}^{A}{\bf e}_{y}y}   & {}^{0}z_{{}^{A}{\bf e}_{z}y}  \\
{}^{0}x_{{}^{A}{\bf e}_{x}z}  & {}^{0}y_{{}^{A}{\bf e}_{y}z}   & {}^{0}z_{{}^{A}{\bf e}_{z}z}
\end{array} \right]
\left[ \begin{array}{c}
0 \\
0 \\
1
\end{array} \right] \\
&=&
\left[ \begin{array}{ccc}
{}^{0}x_{{}^{A}{\bf e}_{x}x}  & {}^{0}y_{{}^{A}{\bf e}_{y}x}   & {}^{0}z_{{}^{A}{\bf e}_{z}x}  \\
{}^{0}x_{{}^{A}{\bf e}_{x}y}  & {}^{0}y_{{}^{A}{\bf e}_{y}y}   & {}^{0}z_{{}^{A}{\bf e}_{z}y}  \\
{}^{0}x_{{}^{A}{\bf e}_{x}z}  & {}^{0}y_{{}^{A}{\bf e}_{y}z}   & {}^{0}z_{{}^{A}{\bf e}_{z}z}
\end{array} \right]
\left(
{}^{A}p_{x}{}^{A}{\bf e}_{x} +
{}^{A}p_{y}{}^{A}{\bf e}_{y} +
{}^{A}p_{z}{}^{A}{\bf e}_{z}
\right)
\end{array} $$

最終的に以下のように表せます。

$$
\begin{array}{rcl}
{}^{0}{\bf p} &=&
\left[ \begin{array}{c}
{}^{0}{\bf x}_{{}^{A}{\bf e}_{x}} &
{}^{0}{\bf y}_{{}^{A}{\bf e}_{y}} &
{}^{0}{\bf z}_{{}^{A}{\bf e}_{z}}
\end{array} \right]
\left(
{}^{A}p_{x}{}^{A}{\bf e}_{x} +
{}^{A}p_{y}{}^{A}{\bf e}_{y} +
{}^{A}p_{z}{}^{A}{\bf e}_{z}
\right) \\
&=&
\left[ \begin{array}{c}
{}^{0}{\bf x}_{{}^{A}{\bf e}_{x}} &
{}^{0}{\bf y}_{{}^{A}{\bf e}_{y}} &
{}^{0}{\bf z}_{{}^{A}{\bf e}_{z}}
\end{array} \right]
{}^{A}{\bf p } \\
&=&
{}^{0}{\bf R}_{A}\ {}^{A}{\bf p }
\end{array}
$$

基底ベクトルは座標値だけみると、\( {}^{A}{\bf e}_{x} \)も\( {}^{0}{\bf e}_{x} \)も同じ座標値\( \left[ \begin{array}{ccc} 1 & 0 & 0 \end{array} \right] \) ですが、両者は別モノですね。

座標値を表す座標系空間が異なるということを忘れて同じと思ってしまう時もありますが。

上の式は、座標系\( \Sigma_{A} \)空間上のベクトル\( {}^{A}{\bf p } \)が、\( {}^{0}{\bf R}_{A} \)によって座標系\( \Sigma_{0} \)空間上のベクトル\( {}^{0}{\bf p } \)に変換されていることを表しているのです。

さらに行列\( {}^{0}{\bf R}_{A} \)の中身は、

座標系\( \Sigma_{A} \)の基底ベクトル\( {}^{A}{\bf e}_{x} \), \( {}^{A}{\bf e}_{y} \), \( {}^{A}{\bf e}_{z} \)を、絶対座標系\( \Sigma_{0} \)基準で表したときのベクトル\( {}^{0}{\bf x}_{{}^{A}{\bf e}_{x}} \), \( {}^{0}{\bf y}_{{}^{A}{\bf e}_{y}} \), \( {}^{0}{\bf z}_{{}^{A}{\bf e}_{z}} \)で構成されているのです。

$$
{}^{0}{\bf R}_{A}
=
\left[ \begin{array}{c}
{}^{0}{\bf x}_{{}^{A}{\bf e}_{x}} &
{}^{0}{\bf y}_{{}^{A}{\bf e}_{y}} &
{}^{0}{\bf z}_{{}^{A}{\bf e}_{z}}
\end{array} \right]
$$

このベクトル\( {}^{0}{\bf x}_{{}^{A}{\bf e}_{x}} \), \( {}^{0}{\bf y}_{{}^{A}{\bf e}_{y}} \), \( {}^{0}{\bf z}_{{}^{A}{\bf e}_{z}} \)は、
座標系\( \Sigma_{A} \)原点が絶対座標系\( \Sigma_{0} \)原点からベクトル\( {}^{0}{\bf p}_{A} \)だけ離れていると、
下図のように各ベクトルの大きさは、座標系\( \Sigma_{0} \)から\( \Sigma_{A} \)への並進移動分のベクトル\( {}^{0}{\bf p}_{A} \)がどのような値をとるかによってバラバラです。(手書きで見苦しくて申し訳ないです)

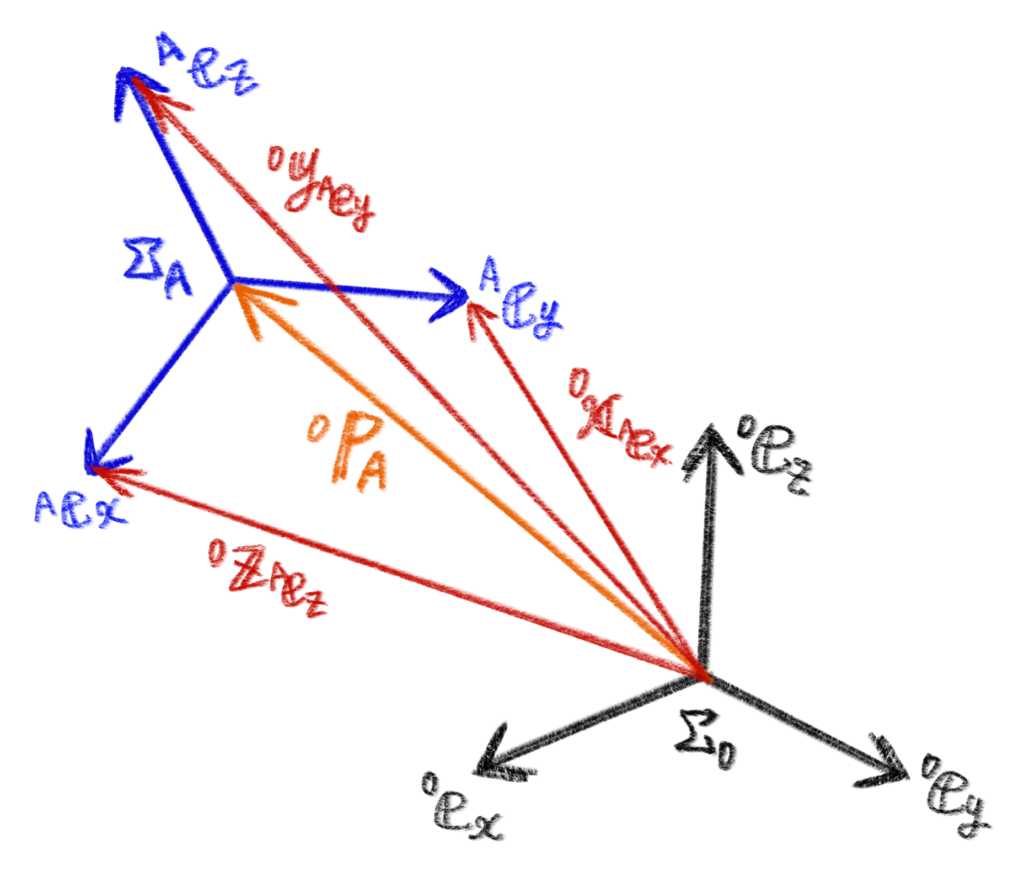
今は回転のみを考えたいので、並進ベクトル\( {}^{0}{\bf p}_{A} \)は無視して、
下図のように座標系\( \Sigma_{A} \)原点が絶対座標系\( \Sigma_{0} \)原点と一致するように考えます。
(これまた手書きで見苦しくて申し訳ないです)

絶対座標系\( \Sigma_{0} \)を、回転軸\( \bf n \)まわりに回転角\( \theta \)だけ回転した座標系が、\( \Sigma_{A} \)と見ることができます。

絶対座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{A} \)の基底ベクトル\( {}^{A}{\bf e}_{x} \), \( {}^{A}{\bf e}_{y} \), \( {}^{A}{\bf e}_{z} \)は、\( {}^{0}{\bf x}_{{}^{A}{\bf e}_{x}} \), \( {}^{0}{\bf y}_{{}^{A}{\bf e}_{y}} \), \( {}^{0}{\bf z}_{{}^{A}{\bf e}_{z}} \)にそのまま対応するので
各ベクトルの大きさは１になります。

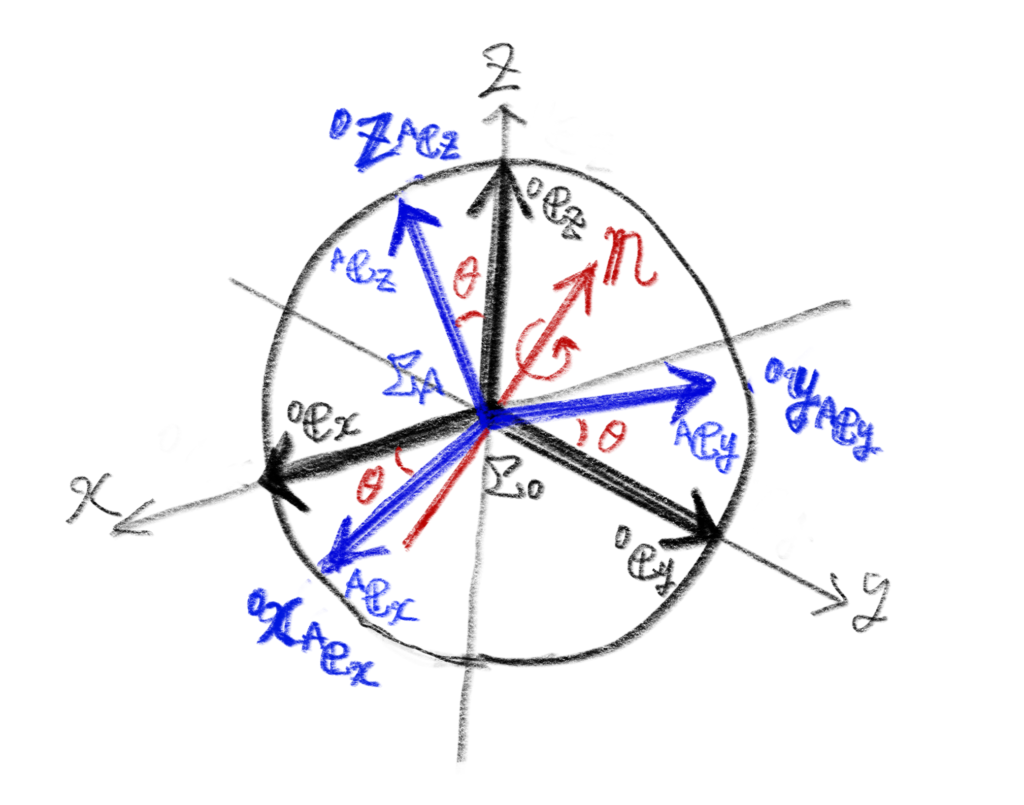
行列\( {}^{0}{\bf R}_{A} \)は、
座標系\( \Sigma_{A} \)の基底ベクトル\( {}^{A}{\bf e}_{x} \), \( {}^{A}{\bf e}_{y} \), \( {}^{A}{\bf e}_{z} \)を絶対座標系\( \Sigma_{0} \)基準で表したベクトル\( {}^{0}{\bf x}_{{}^{A}{\bf e}_{x}} \), \( {}^{0}{\bf y}_{{}^{A}{\bf e}_{y}} \), \( {}^{0}{\bf z}_{{}^{A}{\bf e}_{z}} \)で構成されており、
これは座標系\( \Sigma_{A} \)の回転状態、いわゆる姿勢を表しているといえるのです。

（意味１）回転行列は座標系の姿勢を表す

また、先程の式変形で以下のような関係があることを示しました。

$$
{}^{0}{\bf p} = {}^{0}{\bf R}_{A}\ {}^{A}{\bf p }
$$

回転行列\( {}^{0}{\bf R}_{A} \)が、座標系\( \Sigma_{A} \)基準のベクトル\( {}^{A}{\bf p} \)にかかると(作用すると)、座標系\( \Sigma_{A} \)基準のベクトル\( {}^{0}{\bf p} \)に変換されるのでした。

回転行列は、それ自体は座標系の姿勢を表していますが、その座標系基準で表されたベクトルに作用すると、座標系変換の作用を持ちます。

（意味２）回転行列は座標系変換の作用をもつ

ふう、、

回転行列は奥が深い。

でもまだ実は座標系変換だけでなく、もう一つ、回転行列の作用がもつ意味があります。

それが回転運動です。

座標系の基底ベクトルの回転運動

（意味３）回転行列は回転運動の作用をもつ

今まで、座標系を\( \bf A \)というラベルで表してきましたが、これを今度は時間\( t \)に置き換えて考えてみます。

時々刻々と変化する回転運動を、先程まで説明してきた座標系変換のように考えます。

時刻\( t \)のときの絶対座標系\( \Sigma_{0} \)基準でベクトル \( {}^{0}{\bf p}(t) \)だったものが、

時間\( \Delta t \)のあいだ\(\Delta \theta \)回転して

時刻\( t + \Delta \)のときの絶対座標系\( \Sigma_{0} \)基準でベクトル \( {}^{0}{\bf p}(t + \Delta) \)になったとします。

この運動を式で表すと以下のように書けます。

$$
\begin{array}{rcl}
{}^{0_{t+\Delta t}}{\bf p}(t + \Delta t) &=& {}^{0_{t + \Delta t}}{\bf R}_{0_t}( \Delta t ) {}^{0_t}{\bf p}(t) \\
\end{array}
$$

冒頭にも述べましたが、回転行列\( \bf R \)の直接の入力は回転角\( \theta \)です（回転角\( \theta \)の入力が時間t）。

時間\( \Delta t \)のあいだ回転するとき、回転角が\( \Delta \theta \)とすると、上の式は以下のように直せます。

$$
{}^{0_{t + \Delta t}}{\bf p}(t + \Delta t) = {}^{0_{t + \Delta t}}{\bf R}_{0_t}( \Delta \theta) {}^{0_t}{\bf p}(t)
$$

以降、時刻\( t + \Delta t \)のときの絶対座標系\( \Sigma_{0} \)基準という表現は、省略して以下のように書かせてもらいます。

$$
{}^{0}{\bf p}(t + \Delta t) = {}^{0}{\bf R}( \Delta \theta) {}^{0}{\bf p}(t)
$$

絶対座標系\( \Sigma_{0} \)基準の基底ベクトル\( {}^{0}{\bf e}_{x} \), \( {}^{0}{\bf e}_{y} \), \( {}^{0}{\bf e}_{z} \)は、回転角\( \Delta \theta \)に伴って\( {}^{0}{\bf x}_{{}^{0}{\bf e}_{x}}(\Delta \theta) \), \( {}^{0}{\bf y}_{{}^{0}{\bf e}_{y}}(\Delta \theta) \), \( {}^{0}{\bf z}_{{}^{0}{\bf e}_{z}} (\Delta \theta) \)となるので、姿勢の変化は以下のようになります。

$$
{}^{0}{\bf R} (\Delta \theta)
=
\left[ \begin{array}{c}
{}^{0}{\bf x}_{{}^{0}{\bf e}_{x}} (\Delta \theta) &
{}^{0}{\bf y}_{{}^{0}{\bf e}_{y}} (\Delta \theta) &
{}^{0}{\bf z}_{{}^{0}{\bf e}_{z}} (\Delta \theta)
\end{array} \right]
$$

さらにこれら基底ベクトル\( {}^{0}{\bf x}_{{}^{0}{\bf e}_{x}} \), \( {}^{0}{\bf y}_{{}^{0}{\bf e}_{y}} \), \( {}^{0}{\bf z}_{{}^{0}{\bf e}_{z}} \)は、下図のように\( \Delta \theta \)変化すると、原点は同じまま、かつベクトルの大きさは１なので、半径１の球の表面上の点を移動します。

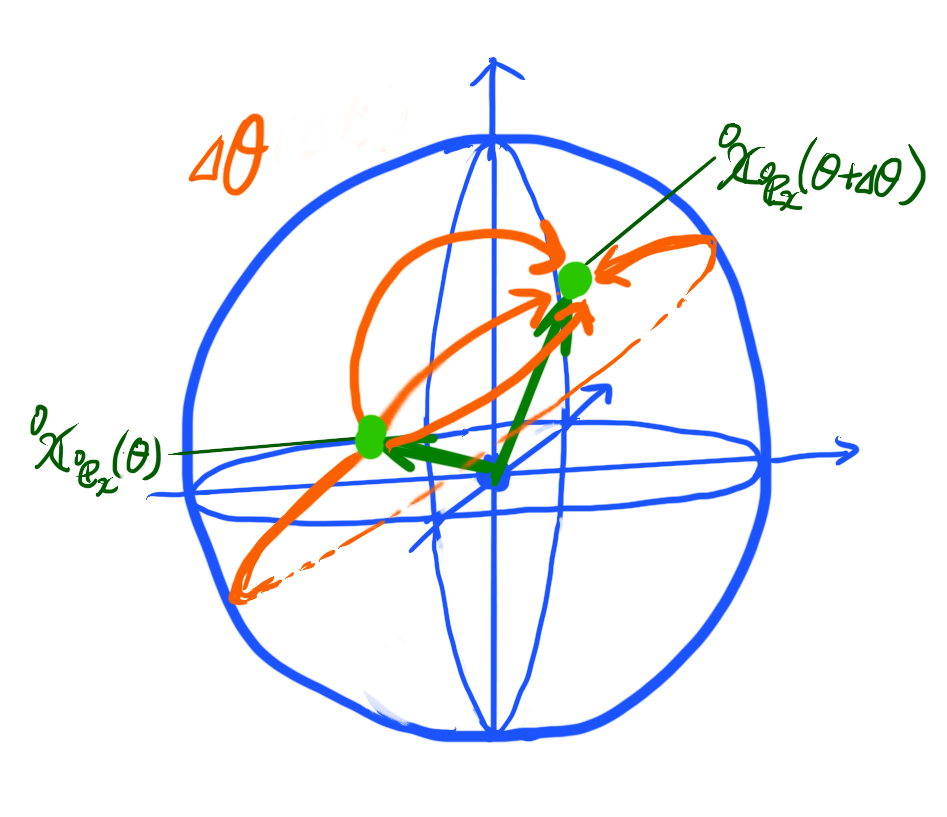
図にもオレンジの線でいくつか描きましたが、この基底ベクトルの球表面上での移動の仕方は、一様ではありません。

\( \Delta \theta \)の軌道(＝\( \theta(t) \)の軌道計算方法)、回転軸方向\( \bf n \)に依存します。

よって、姿勢の変化\( {}^{0}{\bf R}(\Delta \theta) \)も\( \theta(t) \)の軌道、回転軸方向\( \bf n \)に依存することになります。
これは \( \Delta {\bf \omega}  = \Delta t \ {\bf \omega}(t) = \Delta \theta \ {\bf n} \)に依存すると言うこともできます。ロドリゲスの公式を当てはめると姿勢の変化とは\( {}^{0}{\bf R}(\Delta \theta, {\bf n}) \)として以下のように書き表わすこともできます。

$$
\begin{array}{rcl}
{}^{0}{\bf R}(\Delta \theta)
&=&
\left[ \begin{array}{c}
{}^{0}{\bf x}_{{}^{0}{\bf e}_{x}} (\Delta \theta) &
{}^{0}{\bf y}_{{}^{0}{\bf e}_{y}} (\Delta \theta) &
{}^{0}{\bf z}_{{}^{0}{\bf e}_{z}} (\Delta \theta)
\end{array} \right] \\
&=& {}^{0}{\bf R} (\Delta \theta, {\bf n}) \\
&=& {\bf I} + {\rm sin}(\Delta \theta) {\bf[ n\times]} + (1 – {\rm cos}(\Delta \theta)) {\bf[ n\times]}^2 \
\end{array}
$$

\( \Delta t \)時間変化後の姿勢、時刻\( t + \Delta t \)のときの姿勢\( {}^{0}{\bf R}(t + \Delta t )\)は以下のように表せます。

$$
\begin{array}{rcl}
{}^{0}{\bf R} (t + \Delta t)
&=& {}^{0}{\bf R} (\Delta \theta, {\bf n}) {}^{0}{\bf R} (t)
\end{array}
$$

開始時刻\( t_0 \) から \( \Delta t \)ずつ経過して 終端時刻 \( t_f \) まで姿勢の運動は以下のように書き表せることができると言えます。

$$
\begin{array}{rcl}
{}^{0}{\bf R} (t_f)
&=& {}^{0}{\bf R}_{f-1 \rightarrow f}(\Delta t) \cdots {}^{0}{\bf R}_{i \rightarrow i+1}(\Delta t) \cdots {}^{0}{\bf R}_{1 \rightarrow 2}(\Delta t) {}^{0}{\bf R}_{0 \rightarrow 1}(\Delta t) {}^{0}{\bf R}(t_0) \\
&=& {}^{0}{\bf R}(\Delta \theta_f) \cdots {}^{0}{\bf R}(\Delta \theta_i) \cdots {}^{0}{\bf R}(\Delta \theta_2) {}^{0}{\bf R}(\Delta \theta_1) {}^{0}{\bf R}(t_0) \\
&=& {}^{0}{\bf R}(\Delta \theta_f, {\bf n}_f) \cdots {}^{0}{\bf R}(\Delta \theta_i, {\bf n}_i) \cdots {}^{0}{\bf R}(\Delta \theta_2, {\bf n}_2) {}^{0}{\bf R}(\Delta \theta_1, {\bf n}_1) {}^{0}{\bf R}(t_0)
\end{array}
$$

回転行列の速度

以上を踏まえて、回転行列の速度\( {\dot {\bf R}} \)が何かを考えると、

姿勢の速度

と簡単に考えられます。

姿勢は基底ベクトルで構成されていたので、姿勢の速度とは基底ベクトルの速度\( {}^{0}{\dot {\bf x}}_{{}^{0}{\bf e}_{x}} \), \( {}^{0}{\dot {\bf y}}_{{}^{0}{\bf e}_{y}} \), \( {}^{0}{\dot {\bf z}}_{{}^{0}{\bf e}_{z}} \)といえます。

言い換えると、

基底ベクトルの運動方向(球表面上を移動する軌道の接線の傾き)

を表しています。

これらは、回転角の軌道速度\( {\dot \theta}(t) \)、回転軸方向\( \bf n \)に依存します。

この特徴をまとめたものが、角速度ベクトル\( \bf \omega \)だったのですね。

$$
{\bf \omega} = {\dot \theta} {\bf n}
$$

速度\( {\dot {\bf R}} \)の式を見直してみると、

$$ \begin{array}{rcl}
{\dot {\bf R}} &=& {\dot \theta} [{\bf n} \times] {\bf R} \\
&=& [\omega \times] {\bf R}
\end{array}
$$

でした。

回転行列\( {\bf R} \)と、その速度の元となる角速度ベクトル\( \bf \omega \)との外積で得られる行列、

すなわち、基底ベクトルの運動方向

$$
{}^{0}{\dot {\bf x}}_{{}^{0}{\bf e}_{x}} = \omega \times {}^{0}{\bf x}_{{}^{0}{\bf e}_{x}} = {\dot \theta} {\bf n} \times {}^{0}{\bf x}_{{}^{0}{\bf e}_{x}}
$$

$$
{}^{0}{\dot {\bf y}}_{{}^{0}{\bf e}_{y}} = \omega \times {}^{0}{\bf y}_{{}^{0}{\bf e}_{y}} = {\dot \theta} {\bf n} \times {}^{0}{\bf y}_{{}^{0}{\bf e}_{y}}
$$

$$
{}^{0}{\dot {\bf z}}_{{}^{0}{\bf e}_{z}} = \omega \times {}^{0}{\bf z}_{{}^{0}{\bf e}_{z}} = {\dot \theta} {\bf n} \times {}^{0}{\bf z}_{{}^{0}{\bf e}_{z}}
$$

を表していたのでした。

この運動方向は、外積の性質からもいえるように、回転軸\( \bf n \)と各基底ベクトルと垂直に交わる方向になります。

上の図の、球表面に対して接する方向です。

絶対座標系\( \Sigma_{0} \)から見たベクトル\( {}^{0} {\bf p} \)の速度\( {}^{0}{\dot {\bf p}} \)は、角速度ベクトル \( \bf \omega \) により外積の形で表され、さらにその外積ベクトルは、\( {}^{0}{\dot {\bf R}} \)についての方程式から\( {}^{0}{\dot {\bf R}} {}^{0} {\bf R}^{\rm T} \)となることが分かるので、以下の式で表されます。

$$
\begin{array}{rcl}
{}^{0}{\dot {\bf p}} &=& {\bf \omega} \times {}^{0}{\bf p} \\
&=& [{\bf \omega} \times ] {}^{0}{\bf p} \\
&=& {}^{0}{\dot {\bf R}} {}^{0} {\bf R}^{\rm T} {}^{0}{\bf p}
\end{array}
$$

ふう、、

ここまで回転行列を掘り下げるなんて、まぁまずやらないですね。

「だからどうした」と、実際必要性を全く感じない話かもしれません。

途中の式変形とか狂気の沙汰でしたね。

でも、自分でこうやって深いところまで探った後は、現象を多面的に捉えて理解しやすくなるし、制御するときの応用を考えやすくなるので、一度はやっときたいと考えています。

あと、たいていのロボット工学の教科書では、回転行列の以下の性質

• 姿勢
• 座標系変換させるオペレータ
• 回転運動させるオペレータ

を一緒くたに説明してあり、それぞれの意味・利用方法が違うことがわからなくなります（梶田先生の教科書ではきちんと説明してあります）。

なので今後、回転行列を出すときはどれを表しているか十分注意してノートしていきたいです。

以上です。