こんにちは。だいCです。
これまで一つの回転軸まわりの回転運動だけ考えてきましたが、
今回からはさらに別の回転や並進運動も複合させた運動についても考えていこうと思います。
いずれは連鎖座標系の速度・加速度としてまとめようと思いますが、
まずは、回転&回転、回転&並進の場合で個別に見ていこうと思います。
今回は回転&回転についてノートします。
1. 目的
二つの回転軸まわりの回転運動における、質点の位置姿勢の速度・加速度を求める
2. 二つの回転軸まわりの回転を考える場面
二つの回転軸まわりの回転を考える場面は、いろいろあると思います。
複数関節軸をもつロボットが各軸同時に動作したときに各関節にかかる速度や加速度を知りたいとき、
順動力学について考えるときなどなど。
今回は例として、以下の図のように直交する二つの回転軸をもつロボットを考えます。
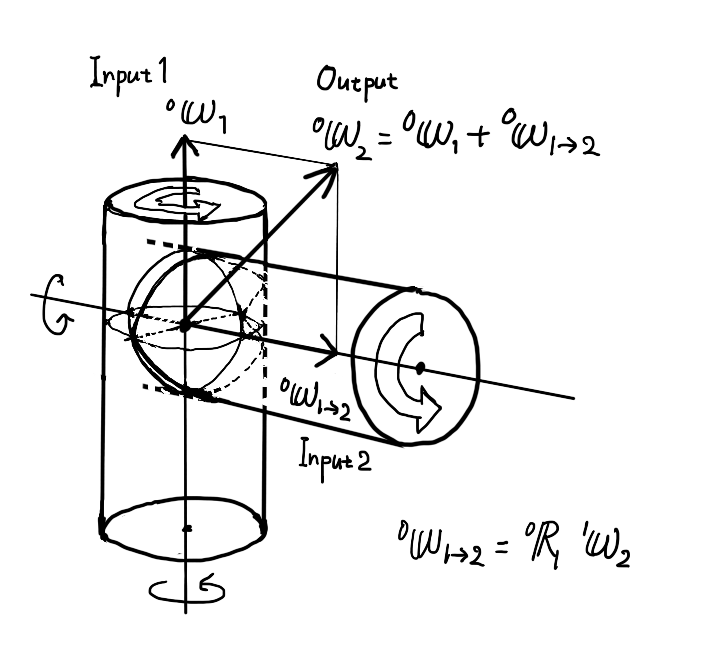
3. 前提
- 二つの回転を回転1、回転2とします。
- 基準座標系を\( \Sigma_{0} \)、回転1と一緒に回る座標系を\( \Sigma_{1} \)、回転2と一緒に回る座標系を\( \Sigma_{2} \)とします。
- 入力1:基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{1} \)の位置\( {}^{0}{\bf p}_{1} \)(一定)
- 入力2:基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{1} \)の姿勢\( {}^{0}{\bf R}_{1} \)
- 入力3:基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{1} \)の角速度ベクトル\( {}^{0}{\bf \omega}_{1} \) ( 回転軸\({}^{0}{\bf n}_{1} \), 角速度\(\dot{\theta_1}\) )
- 入力4:基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{1} \)の角加速度ベクトル\( {}^{0}\dot{\bf \omega}_{1} \) ( 回転軸\({}^{0}{\bf n}_{1} \), 角速度\(\ddot{\theta_1}\) )
- 入力5:座標系\( \Sigma_{1} \)から見た座標系\( \Sigma_{2} \)の位置\( {}^{1}{\bf p}_{2} \)(一定)
- 入力6:座標系\( \Sigma_{1} \)から見た座標系\( \Sigma_{2} \)の姿勢\( {}^{1}{\bf R}_{2} \)(一定)
- 入力7:座標系\( \Sigma_{2} \)から見た、座標系\( \Sigma_{2} \)と一緒に回るある点Pの位置ベクトル\( {}^{2}{\bf p}_{A} \)(一定)
- 入力8:座標系\( \Sigma_{1} \)から見た座標系\( \Sigma_{2} \)の角速度ベクトル\( {}^{1}{\bf \omega}_{2} \) ( 回転軸\({}^{1}{\bf n}_{2} \), 角速度\(\dot{\theta_2}\) )
- 入力9:座標系\( \Sigma_{1} \)から見た座標系\( \Sigma_{2} \)の角加速度ベクトル\( {}^{1}\dot{\bf \omega}_{2} \) ( 回転軸\({}^{1}{\bf n}_{2} \), 角速度\(\ddot{\theta_2}\) )
- 出力1:基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の角速度ベクトル\( {}^{0}{\bf \omega}_{2} \)
- 出力2:基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の位置・姿勢の速度\( {}^{0}\dot{\bf p}_{2} \)、\( {}^{0}\dot{\bf R}_{2} \)
- 出力3:基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の角加速度ベクトル\( {}^{0}\dot{\bf \omega}_{2} \)
- 出力4:基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の位置・姿勢の加速度\( {}^{0}\ddot{\bf p}_{2} \)、\( {}^{0}\ddot{\bf R}_{2} \)
- 二つの回転の効果のみ注目したいので重力加速度を無視します。無重力状態でロボットを動かしているとしましょう。
4. 準備
座標系\(\Sigma_{1}\)基準の座標系\(\Sigma_{2}\)への相対的なベクトルを、座標系\(\Sigma_{0}\)基準に変換すると以下のようになります。
$$
{}^{0}{\bf p}_{1 \rightarrow 2} = {}^{0}{\bf R}_{1} {}^{1}{\bf p}_{2}
$$
角速度ベクトル\(\bf \omega\)についても同じことがいえます。
$$
{}^{0}{\bf \omega}_{1 \rightarrow 2} = {}^{0}{\bf R}_{1} {}^{1}{\bf \omega}_{2}
$$
剛体の運動(回転行列の速度とは)でノートしましたが、
ある位置の点\(\bf p\)とその姿勢\( \bf R \)が角速度ベクトル\(\bf \omega \)で回転すると、その位置と姿勢の速度(\( \dot{\bf p} \), \( \dot{\bf R} \))は以下のように表すことができたのでした。
$$ \begin{array}{rcl}
{\dot {\bf p}} &=& {\bf \omega} \times {\bf p}
\end{array}
$$
$$ \begin{array}{rcl}
{\dot {\bf R}} &=& [{\bf \omega} \times] {\bf R} \\
&=& {\bf \omega} \times {\bf R}
\end{array}
$$
5. 二つの回転軸まわりの回転における位置・姿勢の速度と加速度
座標系\(\Sigma_{0} \)基準の座標系\(\Sigma_{2} \)の位置\( {}^{0}{\bf p}_{2} \)は、入力\( {}^{0}{\bf p}_{1} \)、\( {}^{0}{\bf R}_{1} \)、\( {}^{1}{\bf p}_{2} \)を用いて以下のように求まります。
$$ \begin{array}{rcl}
{}^{0}{\bf p}_{2} &=& {}^{0}{\bf p}_{1} + {}^{0}{\bf p}_{1 \rightarrow 2} \\
&=& {}^{0}{\bf p}_{1} + {}^{0}{\bf R}_{1}{}^{1}{\bf p}_{2}
\end{array}
$$
座標系\(\Sigma_{0} \)基準の座標系\(\Sigma_{2} \)の姿勢\( {}^{0}{\bf R}_{2} \)は、入力\( {}^{0}{\bf R}_{1} \)、\( {}^{1}{\bf R}_{2} \)を用いて以下のように求まります。
$$ \begin{array}{rcl}
{}^{0}{\bf R}_{2} = {}^{0}{\bf R}_{1} {}^{1}{\bf R}_{2}
\end{array}
$$
以降、この\( {}^{0}{\bf p}_{2} \)、\( {}^{0}{\bf R}_{2} \)を用います。
準備で述べたとおり、座標系\(\Sigma_{1} \)基準で見た回転する座標系\( \Sigma_{2}\)の相対的な回転速度ベクトル\( {}^{1}{\bf \omega}_{2} \)は、
座標系\(\Sigma_{0} \)基準\( {}^{0}{\bf \omega}_{1 \rightarrow 2} \)に変換すると以下のようになります。
$$
{}^{0}{\bf \omega}_{1 \rightarrow 2} = {}^{0}{\bf R}_{1} {}^{1}{\bf \omega}_{2}
$$
これを用いて、座標系\(\Sigma_{0} \)基準で見た回転する座標系\( \Sigma_{2}\)の回転速度ベクトル\( {}^{0}{\bf \omega}_{2} \)は、ベクトルの合成により以下のように表せます。
$$
{}^{0}{\bf \omega}_{2} = {}^{0}{\bf \omega}_{1} + {}^{0}{\bf \omega}_{1 \rightarrow 2}
$$
準備で述べたとおり、
座標系\( \Sigma_{0} \)基準で見た回転する座標系\( \Sigma_{2} \)上の位置の点\( {}^{0}{\bf p}_{2} \)とその姿勢\( {}^{0}{\bf R}_{2} \)が角速度ベクトル\({}^{0}{\bf \omega}_{2} \)で回転したとき、
その位置と姿勢の速度(\( {}^{0}{\dot{\bf p}}_{2} \), \( {}^{0}{\dot{\bf R}}_{2} \))は、それらの外積で求まるため、以下のように表せます。
$$ \begin{array}{rcl}
{}^{0}{\dot {\bf p}}_{2} &=& {}^{0}{\bf \omega}_{2} \times {}^{0}{\bf p}_{2} \\
&=& {}^{0}{\bf \omega}_{2} \times ( {}^{0}{\bf p}_{1} + {}^{0}{\bf p}_{1 \rightarrow 2} + {}^{0}{\bf p}_{2 \rightarrow 2} ) \\
&=& {}^{0}{\bf \omega}_{2} \times {}^{0}{\bf p}_{1 \rightarrow 2} + {}^{0}{\bf \omega}_{2} \times {}^{0}{\bf p}_{2 \rightarrow 2} \\
&=& ( {}^{0}{\bf \omega}_{1} + {}^{0}{\bf \omega}_{1 \rightarrow 2} ) \times {}^{0}{\bf p}_{1 \rightarrow 2} + ( {}^{0}{\bf \omega}_{1} + {}^{0}{\bf \omega}_{1 \rightarrow 2} ) \times {}^{0}{\bf p}_{2 \rightarrow 2} \\
&=& {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf p}_{1 \rightarrow 2}
\end{array}
$$
$$ \begin{array}{rcl}
{}^{0}\dot{\bf R}_{2} &=& {}^{0}{\bf \omega}_{2} \times {}^{0}{\bf R}_{2}
\end{array}
$$
ただし注意が必要な点として、角速度ベクトル \({\bf \omega}_{2}\) によって発生する並進速度 \({}^{0}{\dot {\bf p}}_{2}\) は、位置 \({}^{0}{\bf p}_{2} = {}^{0}{\bf p}_{1} + {}^{0}{\bf p}_{1 \rightarrow 2} + {}^{0}{\bf p}_{2 \rightarrow 2}\) の変位成分のうち角速度ベクトル \({\bf \omega}_{2}\) の回転を受ける成分のみです。 \({}^{0}{\bf p}_{1}\) は回転前の変位であるため関与しません。発生する速度はゼロです。\({}^{0}{\bf p}_{1 \rightarrow 2}\) は、角速度ベクトル \({}^{0}{\bf \omega}_{2}\)のうち \({}^{0}{\bf \omega}_{1}\) の回転を受けますが、 \({}^{0}{\bf \omega}_{1 \rightarrow 2}\) については座標系 \(\Sigma_{2}\) 以降の回転でありこれには関与しません。 \({}^{0}{\bf \omega}_{1 \rightarrow 2}\) の回転を受けるのは \({}^{0}{\bf p}_{2 \rightarrow 2}\) ですが、これは座標系 \(\Sigma_{2}\) 原点であり変位がゼロであるため速度もゼロです。
少し補足になりますが、導出の順序を入れ替えて、\({}^{0}{\bf R}_{2}\)の入力\( {}^{0}{\bf R}_{1} \)、\( {}^{1}{\bf R}_{2} \)との関係から微分して、\({}^{0}{\bf \omega}_{2}\)を導出することもできます。
$$ \begin{array}{rcl}
{}^{0}\dot{\bf R}_{2} &=& \frac{d}{dt} \left( {}^{0}{\bf R}_{1} {}^{1}{\bf R}_{2} \right) \\
&=& {}^{0}{\dot{\bf R}}_{1} {}^{1}{\bf R}_{2} + {}^{0}{\bf R}_{1} {}^{1}{\dot{\bf R}}_{2} \\
&=& [{}^{0}{\omega}_{1} \times] {}^{0}{\bf R}_{1} {}^{1}{\bf R}_{2} + {}^{0}{\bf R}_{1} [{}^{1}{\omega}_{2} \times]{}^{1}{\bf R}_{2} \\
&=& [{}^{0}{\omega}_{1} \times] {}^{0}{\bf R}_{1} {}^{1}{\bf R}_{2} + [ \left( {}^{0}{\bf R}_{1}{}^{1}{\omega}_{2} \right) \times] {}^{0}{\bf R}_{1}{}^{1}{\bf R}_{2} \\
&=& [{}^{0}{\omega}_{1} \times] {}^{0}{\bf R}_{2} + [ {}^{0}{\omega}_{1 \rightarrow 2} \times] {}^{0}{\bf R}_{2} \\
&=& [\left( {}^{0}{\omega}_{1} + {}^{0}{\omega}_{1 \rightarrow 2} \right) \times] {}^{0}{\bf R}_{2} \\
&=& [{}^{0}{\bf \omega}_{2} \times] {}^{0}{\bf R}_{2} \\
&=& {}^{0}{\bf \omega}_{2} \times {}^{0}{\bf R}_{2}
\end{array}
$$
外積と行列の性質から、第三式目から第四式目の変形でだいぶトリッキーな計算をしていますが、第六式目から第七式目の変形より、
$$
{}^{0}{\bf \omega}_{2} = {}^{0}{\bf \omega}_{1} + {}^{0}{\bf \omega}_{1 \rightarrow 2}
$$
と表すことができました。補足終わりです。
剛体の運動(回転運動の速度・加速度・躍度)でやったように、
速度を微分することで、点の位置・姿勢の加速度を求めます。
$$ \begin{array}{rcl}
{}^{0}\ddot{\bf p}_{2} &=& \
{}^{0}{\dot{\bf \omega}}_{2} \times {}^{0}{\bf p}_{2} \
+ {}^{0}{\bf \omega}_{2} \times \left( {}^{0}{\bf \omega}_{2} \times {}^{0}{\bf p}_{2} \right) \\
\end{array}
$$
$$ \begin{array}{rcl}
{}^{0}\ddot{\bf R}_{2} &=& \
{}^{0}{\dot{\bf \omega}}_{2} \times {}^{0}{\bf R}_{2} \
+ {}^{0}{\bf \omega}_{2} \times \left( {}^{0}{\bf \omega}_{2} \times {}^{0}{\bf R}_{2} \right) \\
\end{array}
$$
第二項目は上で求めた\( {}^{0}{\bf \omega}_{2} \)、\( {}^{0}{\bf R}_{2} \)により求められます。加速方向はベクトル\( {}^{0}{\bf \omega}_{2} \)軸に向かう方向で、求心加速度です。
第一項目の角加速度\( {}^{0}{\dot{\bf \omega}}_{2} \)について、さらに、角速度ベクトル\( {}^{0}{\bf \omega}_{2} \)を\( {}^{0}{\bf \omega}_{1} \)、\( {}^{0}{\bf \omega}_{1 \rightarrow 2} \)に分解して求めてみます。
$$ \begin{array}{rcl}
{}^{0}{\dot{\bf \omega}}_{2} \
&=& \
\frac{d}{dt} \left( {}^{0}{\bf \omega}_{1} + {}^{0}{\bf \omega}_{1 \rightarrow 2} \right) \\
&=& \
{}^{0}{\dot{\bf \omega}}_{1} + {}^{0}{\dot{\bf \omega}}_{1 \rightarrow 2} \\
&=& \
{}^{0}{\dot{\bf \omega}}_{1} + \frac{d}{dt} \left( {}^{0}{\bf R}_{1} {}^{1}{\bf \omega}_{2} \right) \\
&=& \
{}^{0}{\dot{\bf \omega}}_{1} + {}^{0}{\dot{\bf R}}_{1} {}^{1}{\bf \omega}_{2} + {}^{0}{\bf R}_{1} {}^{1}{\dot{\bf \omega}}_{2} \\
&=& \
{}^{0}{\dot{\bf \omega}}_{1} + {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf \omega}_{2} + {}^{0}{\bf R}_{1} {}^{1}{\dot{\bf \omega}}_{2} \\
&=& \
{}^{0}{\dot{\bf \omega}}_{1} + {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf \omega}_{1 \rightarrow 2} + {}^{0}{\bf R}_{1} {}^{1}{\dot{\bf \omega}}_{2} \\
\end{array}
$$
第一項目は、座標系\( \Sigma_{0} \)基準の座標系\( \Sigma_{1} \)の角加速度、
第三項目は、座標系\( \Sigma_{1} \)基準の座標系\( \Sigma_{2} \)の角加速度を、座標系\( \Sigma_{0} \)基準に変換したものといえます。
第二項目は、入力の角速度\( {}^{0}{\bf \omega}_{1} \)と\( {}^{0}{\bf \omega}_{1 \rightarrow 2} \)の外積になっています。回転1と回転2が一定角速度で回転する場合、第一項目、第三項目のような角加速度は0になりますが、第二項目の加速度は残ります。
この第二項目の角加速度\( {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf \omega}_{1 \rightarrow 2} \)の意味について考えてみましょう。
以下の図に、ある点\( {}^{0}{\bf p} \)に働く加速度\( {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf \omega}_{1 \rightarrow 2} \)(図中オレンジ)のイメージを描いてみました。
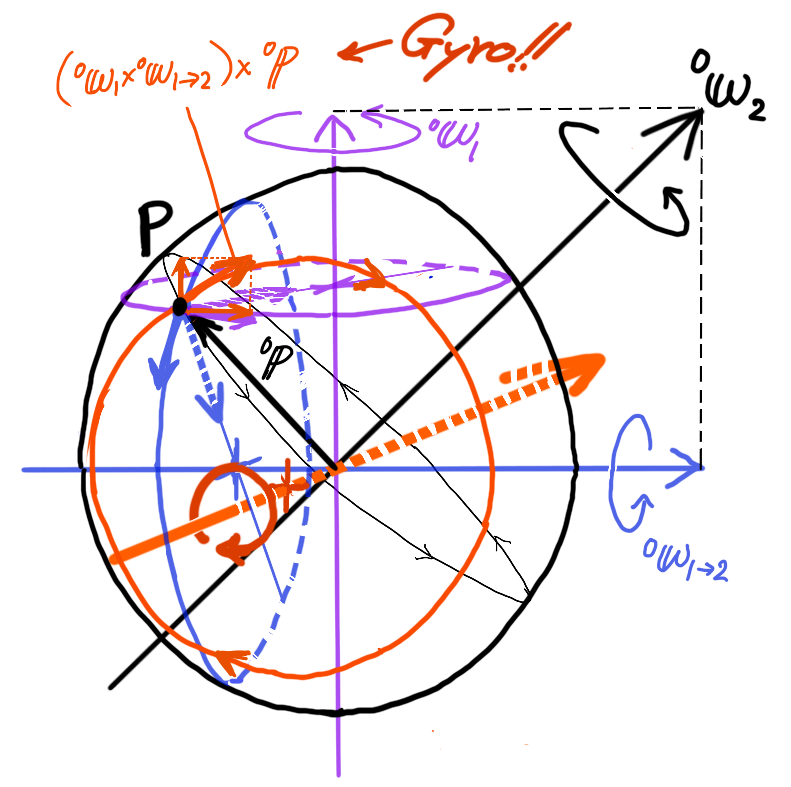
角速度ベクトル\( {}^{0}{\bf \omega}_{1} \)の回転1の運動と、その回転(座標系\( \Sigma_{1} \))上で角速度ベクトル\( {}^{0}{\bf \omega}_{1 \rightarrow 2} \)(座標系\( \Sigma_{0} \)基準)まわりに回転する回転2の運動が合成されて、結果として角速度ベクトル\( {}^{0}{\bf \omega}_{2} \)まわりに回転しているとします。
点Pを合成の角速度ベクトル\( {}^{0}{\bf \omega}_{2} \)まわりに回転するには、図中紫色のベクトル\( {}^{0}{\bf \omega}_{1} \)と青色のベクトル\( {}^{0}{\bf \omega}_{1 \rightarrow 2} \)まわりにそれぞれ回転するための加速度を必要とし、さらに両方の角速度ベクトルに直交するオレンジ色のベクトル軸(奥へと中心を貫通してる矢印)まわりの加速度を必要とします。
この加速度は、図中点Pから出るオレンジ色の矢印によって表されています。
分解すると、図の上方向である回転1の角速度ベクトル\( {}^{0}{\bf \omega}_{1} \)軸方向と、その回転円接線方向にそれぞれ働く加速度が点Pには必要だとわかります。
無重力状態で質量をもった物体が同じ2軸の回転運動をした時、この点Pから出るオレンジ色方向の必要な加速度(力)を与えないと、その反対方向に慣性力が働き、合成された回転の角速度ベクトル\( {}^{0}{\bf \omega}_{2} \)の軸を回転1のベクトル\( {}^{0}{\bf \omega}_{1} \)方向に戻そうとしてしまいます。
すなわち回転2を打ち消す加速度(力)が働きます。
この物理現象をジャイロ効果(gyro effect)と呼ぶそうです。
重力下だと、図中点Pから出るオレンジ色の矢印の、分解した上方向の力と重力が一部相殺され、回転円接線方向のみ残るため、合成された回転の角速度ベクトル\( {}^{0}{\bf \omega}_{2} \)の軸を、ベクトル\( {}^{0}{\bf \omega}_{1} \)軸まわりに回転させる力が働くことがわかります。
これが独楽(こま)などの歳差運動(precession)の原理です。
6. まとめ(二つの回転軸まわりの回転運動における、質点の位置姿勢の速度・加速度)
まとめます。
ステップ1. 座標系\(\Sigma_{0} \)基準の座標系\(\Sigma_{2} \)の位置\( {}^{0}{\bf p}_{2} \)、姿勢\( {}^{0}{\bf R}_{2} \)
座標系\(\Sigma_{0} \)基準の座標系\(\Sigma_{2} \)の位置\( {}^{0}{\bf p}_{2} \)を、入力\( {}^{0}{\bf p}_{1} \)、\( {}^{0}{\bf R}_{1} \)、\( {}^{1}{\bf p}_{2} \)を用いて以下のように求めます。
$$ \begin{array}{rcl}
{}^{0}{\bf p}_{2} = {}^{0}{\bf p}_{1} + {}^{0}{\bf R}_{1}{}^{1}{\bf p}_{2} \\
\end{array}
$$
座標系\(\Sigma_{0} \)基準の座標系\(\Sigma_{2} \)の姿勢\( {}^{0}{\bf R}_{2} \)を、入力\( {}^{0}{\bf R}_{1} \)、\( {}^{1}{\bf R}_{2} \)を用いて以下のように求めます。
$$ \begin{array}{rcl}
{}^{0}{\bf R}_{2} = {}^{0}{\bf R}_{1} {}^{1}{\bf R}_{2}
\end{array}
$$
ステップ2. 座標系\(\Sigma_{0} \)基準で見た座標系\( \Sigma_{1}\)から\( \Sigma_{2}\)への相対的な角速度ベクトル\( {}^{0}{\bf \omega}_{1 \rightarrow 2} \)
座標系\(\Sigma_{0} \)基準で見た座標系\( \Sigma_{1}\)から座標系\( \Sigma_{2}\)への相対的な回転速度ベクトル\( {}^{0}{\bf \omega}_{1 \rightarrow 2} \)を、入力\( {}^{0}{\bf R}_{1} \)、\({}^{1}{\bf \omega}_{2} \)を用いて以下のように求めます。
$$
{}^{0}{\bf \omega}_{1 \rightarrow 2} = {}^{0}{\bf R}_{1} {}^{1}{\bf \omega}_{2}
$$
ステップ3. (出力1) 基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の角速度ベクトル\( {}^{0}{\bf \omega}_{2} \)
座標系\(\Sigma_{0} \)基準で見た回転する座標系\( \Sigma_{2}\)の回転速度ベクトル\( {}^{0}{\bf \omega}_{2} \)を、入力\( {}^{0}{\bf \omega}_{1} \)とステップ2.で求めた\( {}^{0}{\bf \omega}_{1 \rightarrow 2} \)のベクトルの合成により、以下のように求めます。
$$
{}^{0}{\bf \omega}_{2} = {}^{0}{\bf \omega}_{1} + {}^{0}{\bf \omega}_{1 \rightarrow 2}
$$
ステップ4. (出力2) 基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の位置・姿勢の速度\( {}^{0}\dot{\bf p}_{2} \)、\( {}^{0}\dot{\bf R}_{2} \)
基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の位置・姿勢の速度\( {}^{0}\dot{\bf p}_{2} \)、\( {}^{0}\dot{\bf R}_{2} \)を、ステップ1.で求めた\( {}^{0}{\bf p}_{2} \)、\( {}^{0}{\bf R}_{2} \)、ステップ3.で求めた\( {}^{0}{\bf \omega}_{2} \)により、以下のように求めます。
$$ \begin{array}{rcl}
{}^{0}{\dot {\bf p}}_{2} &=& {}^{0}{\bf \omega}_{2} \times {}^{0}{\bf p}_{2} \\
&=& {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf p}_{1 \rightarrow 2}
\end{array}
$$
$$ \begin{array}{rcl}
{}^{0}\dot{\bf R}_{2} &=& {}^{0}{\bf \omega}_{2} \times {}^{0}{\bf R}_{2}
\end{array}
$$
ステップ5. (出力3) 基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の角加速度ベクトル\( {}^{0}\dot{\bf \omega}_{2} \)
基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の角加速度ベクトル\( {}^{0}\dot{\bf \omega}_{2} \)を、入力\( {}^{0}{\bf R}_{1} \)、\( {}^{0}{\bf \omega}_{1} \)、\( {}^{0}{\dot{\bf \omega}}_{1} \)、\( {}^{1}{\dot{\bf \omega}}_{2} \)と、ステップ2.で求めた\( {}^{0}{\bf \omega}_{1 \rightarrow 2} \)により、以下のように求めます。
$$ \begin{array}{rcl}
{}^{0}{\dot{\bf \omega}}_{2} \
&=& \
{}^{0}{\dot{\bf \omega}}_{1} + {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf \omega}_{1 \rightarrow 2} + {}^{0}{\bf R}_{1} {}^{1}{\dot{\bf \omega}}_{2} \\
\end{array}
$$
回転1と回転2が等角速度で回転するとき、\( {}^{0}\dot{\bf \omega}_{2} \)は、以下のように第二項目のジャイロ効果のみになります。
$$ \begin{array}{rcl}
{}^{0}{\dot{\bf \omega}}_{2} \
&=& \
{}^{0}{\bf \omega}_{1} \times {}^{0}{\bf \omega}_{1 \rightarrow 2} \\
\end{array}
$$
ステップ6. (出力4) 基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の位置・姿勢の加速度\( {}^{0}\ddot{\bf p}_{2} \)、\( {}^{0}\ddot{\bf R}_{2} \)
基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の位置・姿勢の加速度\( {}^{0}\ddot{\bf p}_{2} \)、\( {}^{0}\ddot{\bf R}_{2} \)を、ステップ1.で求めた\( {}^{0}{\bf p}_{2} \)、\( {}^{0}{\bf R}_{2} \)、ステップ3.で求めた\( {}^{0}{\bf \omega}_{2} \)、ステップ5.で求めた\( {}^{0}{\dot{\bf \omega}}_{2} \) により、以下のように求めます。
$$ \begin{array}{rcl}
{}^{0}\ddot{\bf p}_{2} &=& \
{}^{0}{\dot{\bf \omega}}_{2} \times {}^{0}{\bf p}_{2} \
+ {}^{0}{\bf \omega}_{2} \times \left( {}^{0}{\bf \omega}_{2} \times {}^{0}{\bf p}_{2} \right) \\
\end{array}
$$
$$ \begin{array}{rcl}
{}^{0}\ddot{\bf R}_{2} &=& \
{}^{0}{\dot{\bf \omega}}_{2} \times {}^{0}{\bf R}_{2} \
+ {}^{0}{\bf \omega}_{2} \times \left( {}^{0}{\bf \omega}_{2} \times {}^{0}{\bf R}_{2} \right) \\
\end{array}
$$
以上でまとめは終わりです。
7. ジャイロ効果の参考動画
YouTubeを漁るとジャイロ効果に関連する動画はたくさんありますね。ググってすぐ出てきたのをいくつかピックアップしときます。
無重力下の実験動画
NASAの宇宙飛行士Michael E. Fossumさんが、宇宙船での無重力下でジャイロ効果を解説してくれています。
ジャイロ効果により、二つ目の回転が打ち消され、元の回転軸方向に戻ろうとしているのが分かると思います。
3Dモデルで直交2軸回転のジャイロ効果の解説
直感的でわかりやすい動画だったので挙げさせてもらいました。
この動画をアップロードされたJeff Kosmoskiさんは、ググるとKOZM Guitarsというギターのデザイナさんみたいですね。
数式も使わず解説してくれていて、わかりやすいです。
重力下のジャイロ効果いろいろ
重力下のジャイロ効果を応用して、コマの支点に重心位置を合わせたマクスウェルの独楽なんておもちゃもあります。
回転が速いと、支点から重心を結ぶ軸に対し、ジャイロ効果が重力に勝り、その軸を起き上げる方向に力が働き、重心が上に移動する、という現象を逆立ち独楽を分かりやすくして実験してくれてる以下の動画もありました。
あまりこのページでは触れませんが、ジャイロ効果は回転と質量で働く慣性モーメントとして働きます。
逆立ち独楽と同じように、回転している物体が重力を打ち消す現象をわかりやすく試してくれてる動画もありました。
実はこれは、自転車が倒れない仕組みでもあるんですね。
これら不思議な現象も、回転の原理が分かると見てて面白いですね。
リアクションホイール
ジャイロ効果は、宇宙空間の人工衛星の運動制御や、一部移動ロボットの姿勢制御で使われたりします。
最近だとJAXAが三軸姿勢制御モジュールという箱を開発したという記事を見かけたりしましたが、
下にもうちょっと先に記事で見かけたチューリッヒ工科大学(ETH zurich)が開発したCubliを上げておきます。
詳しくはCubliのページで。
このようにジャイロ効果を応用して、機体内部に十分な質量を持ち回転エネルギーをもつ円盤などの回転体(フライホイール)を速度制御して、重心姿勢を制御する装置をリアクションホイールというそうです。
リアクションホイールを使ったロボットといえば、自分の中で一番最初に上がるのは、やはりムラタセイサク君ですね。
「リアクションホイール」という言葉自体、ムラタセイサク君の紹介を見て初めて知った覚えがあります。
ふう、、
今回は、ジャイロ効果の說明をノートしたのですが、関連動画が多めになってしまいました。
他にもブーメランの原理や、ジャイロ効果で遠方まで飛ぶX-Zylo(WMC(William Mark Corporation)製)というおもちゃにも触れたかったのですが、割愛します。
ジャイロ効果の現象は、回転運動の中でも非常に面白い話だと思います。
今回は以上です