こんにちは。だいCです。

 

今回は回転運動によって発生する、直交座標空間上の速度、加速度、躍度についてノートします。

 

1. 目的

一つの回転軸まわりの回転運動における、質点の位置姿勢の速度、加速度、躍度を求める

 

2. 前提

• 運動対象：ある点Pとします。
• 基準座標系：\( \Sigma_{0} \)とします。
• 運動対象の表現：基準座標系\( \Sigma_{0} \)から見た点Pの位置ベクトル\( {}^{0}{\bf p} \)で表現します。
• 入力1(予め既知の情報)：点Pの位置\( {}^{0}{\bf p} \)
• 入力2(予め既知の情報)：角速度ベクトル\( \bf \omega \)(回転軸ベクトル\( \bf n \)、角速度\(\dot{\theta}\) )
• 入力3(予め既知の情報)：角加速度ベクトル\( \dot{\bf \omega} \)(回転軸ベクトル\( \bf n \)、角加速度\(\ddot{\theta}\) )
• 入力4(予め既知の情報)：角躍度ベクトル\( \ddot{\bf \omega} \)(回転軸ベクトル\( \bf n \)、角躍度\( {\theta}^{(3)} \) )
• 出力1(今回算出する情報)：点Pの速度\( {}^{0}\dot{\bf p} \)
• 出力2(今回算出する情報)：点Pの加速度\( {}^{0}\ddot{\bf p} \)
• 出力3(今回算出する情報)：点Pの躍度\( {}^{0}{\bf p}^{(3)} \)

剛体の運動(回転行列の速度とは)で說明しましたが、
\( {}^{0}{\bf p} \)は、基底ベクトル\( {}^{0}{\bf x}_{{}^{0}{\bf e}_{x}}\), \( {}^{0}{\bf y}_{{}^{0}{\bf e}_{y}}\), \( {}^{0}{\bf z}_{{}^{0}{\bf e}_{z}}\)について考えるのと同じです。

 

3. 線形写像―微分

微分して求めていきます。

• 速度は位置の微分
• 加速度は速度の微分
• 躍度は加速度の微分

今回座標系はあまり気にしない話ですが、

一応基準座標系\( O\)を変数左上に記述しておきます。

 

4. 回転運動の速度

回転行列の基底ベクトルの回転速度について考えた時と同じです。

おさらいになりますが、一つの回転軸による回転の角速度ベクトル\( {}^{0}{\bf \omega} \)により、点Pの速度\( {}^{0}{\dot{\bf p}} \)は以下の式で表されます。

$$ \begin{array}{rcl}
{}^{0}{\dot{\bf p}} &=& {}^{0}{\bf \omega} \times {}^{0}{\bf p} \\
&=& [{}^{0}{\bf \omega} \times] {}^{0}{\bf p}
\end{array}
$$

ここで、この速度の方向と大きさについて見てみましょう。

２つのベクトルの外積をとると、

・方向が両ベクトルに直交し且つ掛ける順の右ねじ回転で進む方向となり、

・大きさがその２つのベクトルが張る平行四辺形の面積となるベクトルとなるのでした。

また、大きさ1の回転軸ベクトル\( {}^{0}{\bf n} \)、回転角\( \theta \)により、角速度ベクトルは \( {}^{0}{\bf \omega} = \dot{\theta} {}^{0}{\bf n} \)という定義でした。

以上を踏まえて、速度ベクトル\( {}^{0}{\dot{\bf p}} = {}^{0}{\bf \omega} \times {}^{0}{\bf p} \)の大きさと方向は以下のようになります。

• 方向は、角速度ベクトル\( {}^{0}{\bf \omega} \)の方向=回転軸ベクトル\( \bf n \)の方向と、回転対象の点Pの位置ベクトル\( {}^{0}{\bf p} \)が直交する方向になります。
• 大きさは、回転軸\( {}^{0}{\bf n} \)と位置ベクトル\( {}^{0}{\bf p} \)のなす角を\( \alpha \)とすると、
  $$
  |{}^{0}{\bf \omega} \times {}^{0}{\bf p}| = |{}^{0}{\bf \omega}| |{}^{0}{\bf p}| |{\rm sin}\alpha| = |{\dot{\theta} {}^{0}{\bf n} }| |{}^{0}{\bf p}| |{\rm sin}\alpha| = |\dot{\theta}| |{}^{0}{\bf p}| |{\rm sin}\alpha|
  $$
  さらに点Pと回転軸(直線)の距離 \( r := |{}^{0}{\bf p}| {\rm sin}\alpha \) と置くと、結局大きさは\( |\dot{\theta}| |r| \)となります。

 

5. 回転運動の加速度

加速度\( {}^{0}{\ddot{\bf p}} \)は、速度\( {}^{0}{\dot{\bf p}} \)の微分により以下のように求まります。

$$ \begin{array}{rcl}
{}^{0}{\ddot{\bf p}} &=& \frac{d {}^{0}{\dot{\bf p}} }{dt} \\
&=& \frac{d}{dt} \left( {}^{0}{\bf \omega} \times {}^{0}{\bf p} \right) \\
&=& \frac{d}{dt} \left( {}^{0}{\bf \omega} \right) \times {}^{0}{\bf p} + {}^{0}{\bf \omega} \times \frac{d}{dt} \left({}^{0}{\bf p} \right) \\
&=& {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf p} + {}^{0}{\bf \omega} \times {}^{0}{\dot{\bf p}} \\
&=& {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf p} + {}^{0}{\bf \omega} \times \left( {}^{0}{\bf \omega} \times {}^{0}{\bf p} \right)
\end{array}
$$

ここで、この加速度\( {}^{0}{\ddot{\bf p}} \)の方向と大きさについて見てみましょう。

まず、右辺の第一項、第二項がどのような方向と大きさを指しているか見てみます。

1. 右辺第一項\( {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf p} \)について。
   角速度の微分は\( {}^{0}{\dot{\bf \omega}} =  \ddot{\theta} {}^{0}{\bf n} \)であり、角速度ベクトルに対し方向は、同じ回転軸ベクトル\( {}^{0}{\bf n} \)方向で、大きさが\( \dot{\theta} \)から\( \ddot{\theta} \)に変化したものだとわかります。よって\( {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf p} \)は、
   ・方向は、前節の速度方向と同じ
   ・大きさは、\( \left| {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf p} \right| = |\ddot{\theta}| |r| \)
   となります。
   ちなみに、物理学の教科書や金宮先生(Dragomir N, Nenchev先生)の著書「英語で学ぶロボット工学 ― 運動学，動力学と制御」にもありますが、この加速度のことをtrransverse acceleration(横加速度,オイラー加速度,方位加速度,接線加速度)というそうです(みかけの加速度の呼び名と混同しているかもしれません)。
2. 右辺第二項\( {}^{0}{\bf \omega} \times \left( {}^{0}{\bf \omega} \times {}^{0}{\bf p} \right) \)について。
   ・方向は、前節で見た速度方向と回転軸に直交する方向、さらに言うと軸方向→速度方向へ右ねじに回転させて進む向き、すなわち、点Pから回転軸方向へ垂直に向かう方向となります。
   ・大きさは、\( {}^{0}{\bf \omega} \)と\( \left( {}^{0}{\bf \omega} \times {}^{0}{\bf p} \right) \)のなす角は直交するから\( 90^\circ \)なので、
   $$ \begin{array}{rcl}
   \left| {}^{0}{\bf \omega} \times \left( {}^{0}{\bf \omega} \times {}^{0}{\bf p} \right) \right| &=& |{}^{0}{\bf \omega}| |{}^{0}{\bf \omega} \times {}^{0}{\bf p}| |{\rm sin} 90^\circ| \\
   &=& |\dot{\theta}|\  |\dot{\theta}| |r| \\
   &=& \dot{\theta}^2|r|
   \end{array}
   $$
   となります。
   ちなみにこの加速度は、高校や大学の物理学とかいろんな教科書に出てるようにcentripetal acceleration(求心加速度、向心加速度)というそうです。高校物理だとtransverseの方は習わずこっちしか習わなかったように覚えています。

以上により、

• 加速度\( {}^{0}{\ddot{\bf p}} \)の方向は、もう言葉で說明するのはキツイので、以下のように図に描いてみました。
  

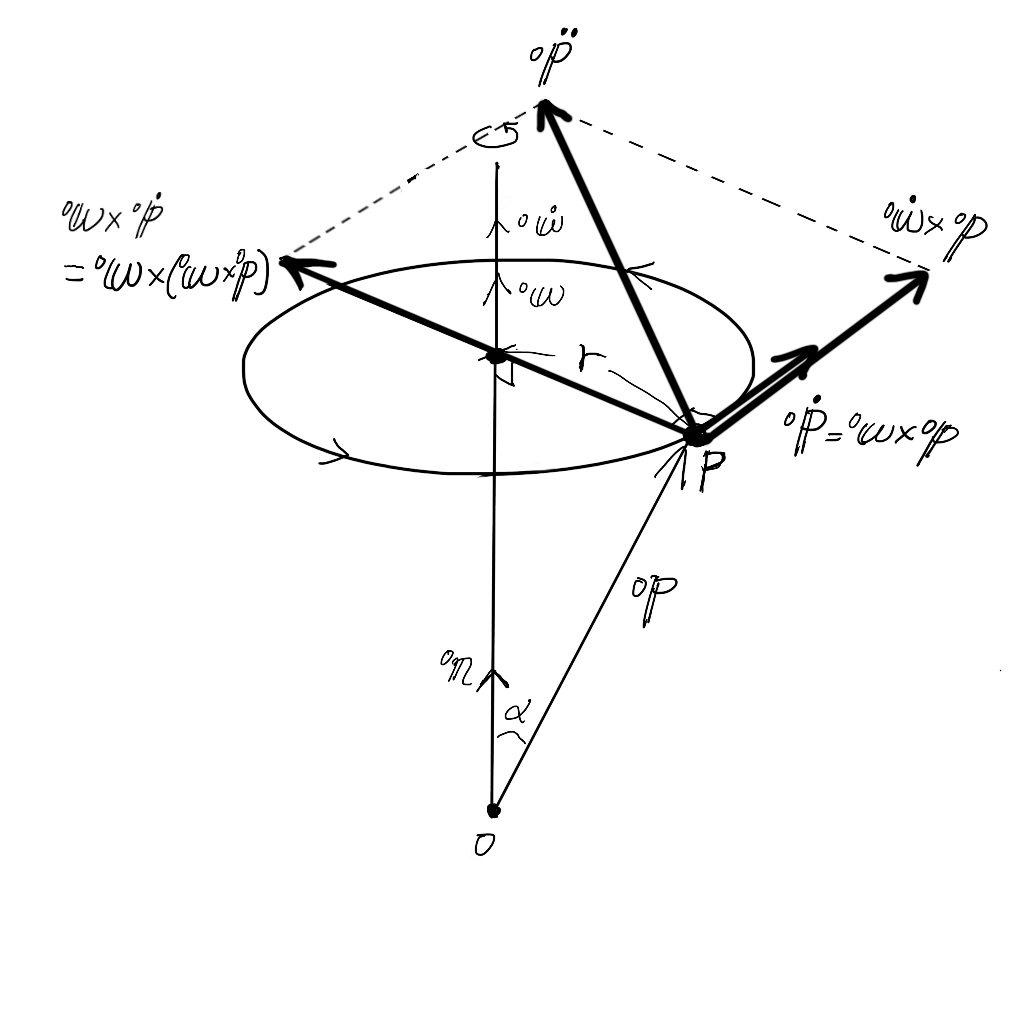
  回転運動の加速度\( {}^{0}{\bf p} \)

• 加速度\( {}^{0}{\ddot{\bf p}} \)の大きさは、右辺第一項、第二項が作る長方形の対角線なので、三平方の定理で出せそうですね。
  大きさについて分解方向で触れている教科書はあるものの、一つに合わせた大きさについて触れているものがないので自己流で以下のように求めました。もし間違ってたらゴメンナサイ。
  $$  \begin{array}{rcl}
  |{}^{0}{\ddot{\bf p}}| &=& \sqrt{ \left| {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf p} \right|^2 + \left| {}^{0}{\bf \omega} \times \left( {}^{0}{\bf \omega} \times {}^{0}{\bf p} \right) \right|^2 } \\
  &=& \sqrt{ \left( |\ddot{\theta}| |r| \right)^2 + \left( \dot{\theta}^2|r| \right)^2 } \\
  &=& |r| \sqrt{ \ddot{\theta}^2 + \dot{\theta}^4 }
  \end{array} $$

 

6. 回転運動の躍度

躍度\( {}^{0}{{\bf p}^{(3)}} \)は、加速度\( {}^{0}{\ddot{\bf p}} \)の微分により以下のように求まります。

$$ \begin{array}{rcl}
{}^{0}{{\bf p}^{(3)}} &=& \frac{d {}^{0}{\ddot{\bf p}} }{dt} \\
&=&  \frac{d}{dt} \left( {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf p} + {}^{0}{\bf \omega} \times {}^{0}{\dot{\bf p}} \right) \\
&=& {}^{0}{\ddot{\bf \omega}} \times {}^{0}{\bf p} + {}^{0}{\dot{\bf \omega}} \times {}^{0}{\dot{\bf p}}
+ {}^{0}{\dot{\bf \omega}} \times {}^{0}{\dot{\bf p}} +  {}^{0}{\bf \omega} \times {}^{0}{\ddot{\bf p}}  \\
&=& {}^{0}{\ddot{\bf \omega}} \times {}^{0}{\bf p} + 2{}^{0}{\dot{\bf \omega}} \times {}^{0}{\dot{\bf p}} + {}^{0}{\bf \omega} \times {}^{0}{\ddot{\bf p}} \\
&=& {}^{0}{\ddot{\bf \omega}} \times {}^{0}{\bf p} + 2{}^{0}{\dot{\bf \omega}} \times \left( {}^{0}{\bf \omega} \times {}^{0}{{\bf p}} \right)
+ {}^{0}{\bf \omega} \times
\left( {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf p} + {}^{0}{\bf \omega} \times \left( {}^{0}{\bf \omega} \times {}^{0}{\bf p} \right) \right) \\
&=& {}^{0}{\ddot{\bf \omega}} \times {}^{0}{\bf p} + 2{}^{0}{\dot{\bf \omega}} \times \left( {}^{0}{\bf \omega} \times {}^{0}{{\bf p}} \right)
+ {}^{0}{\bf \omega} \times
\left( {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf p}
+ \left( {}^{0}{\bf \omega}^{\rm T} {}^{0}{\bf p} \right) {}^{0}{\bf \omega}\ – \ {}^{0}{\bf \omega}^{2}\ {}^{0}{\bf p}  \right) \\
&=& {}^{0}{\ddot{\bf \omega}} \times {}^{0}{\bf p} + 2{}^{0}{\dot{\bf \omega}} \times \left( {}^{0}{\bf \omega} \times {}^{0}{{\bf p}} \right)
+ {}^{0}{\bf \omega} \times \left( {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf p} \right )
+ \left( {}^{0}{\bf \omega}^{\rm T} {}^{0}{\bf p} \right) {}^{0}{\bf \omega} \times {}^{0}{\bf \omega}
\ – \ {}^{0}{\bf \omega}^{2}\  {}^{0}{\bf \omega} \times {}^{0}{\bf p} \\
&=& {}^{0}{\ddot{\bf \omega}} \times {}^{0}{\bf p} + 2{}^{0}{\dot{\bf \omega}} \times \left( {}^{0}{\bf \omega} \times {}^{0}{{\bf p}} \right)
+ {}^{0}{\bf \omega} \times \left( {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf p} \right )
\ – \ {}^{0}{\bf \omega}^{2}\  {}^{0}{\bf \omega} \times {}^{0}{\bf p}
\end{array}
$$

第5式目から第6式目の変形では、外積の公式

$$
{\bf a} \times \left( {\bf b} \times {\bf c} \right) = \left( {\bf a}^{\rm T} {\bf c} \right) {\bf b}\ -\ \left( {\bf a}^{\rm T} {\bf b} \right) {\bf c}
$$

を使っています(これでカッコ部分はスカラーになるので、ベクトルどうしの外積の対象から外してます)。
また、第7式目から第8式目の変形では、同じベクトルどうしの外積はゼロになる性質、

$$
{}^{0}{\bf \omega} \times {}^{0}{\bf \omega} = {\bf 0}
$$

を使っています。

 

 

7. 等角速回転運動(角速度が一定)の場合

角速度が一定だと\( \ddot{\theta} = 0 \)、\({}^{0}\dot{\bf \omega} = {\bf 0}\)になります。

これを踏まえて上述した式を見てみましょう。

高校物理で習ったように、速度、加速度、躍度は次のようになります。

 

7.1. 等角速回転運動のときの速度

上述した\( \dot{{}^{0}{\bf p}}\)と同じ式で表されます。方向も大きさも同じように表せます。

 

7.2. 等角速回転運動のときの加速度

等速回転運動の場合、\({}^{0}\dot{\bf \omega} = {\bf 0}\)になるため、加速度は、回転軸に向かう方向の求心加速度になります。

$$ \begin{array}{rcl}
{}^{0}{\ddot{\bf p}} &=& \frac{d {}^{0}{\dot{\bf p}} }{dt} \\
&=&  {}^{0}{\bf \omega} \times \left( {}^{0}{\bf \omega} \times {}^{0}{\bf p} \right)
\end{array}
$$

• 方向は回転軸に向かう方向で以下の図のようになります。
  

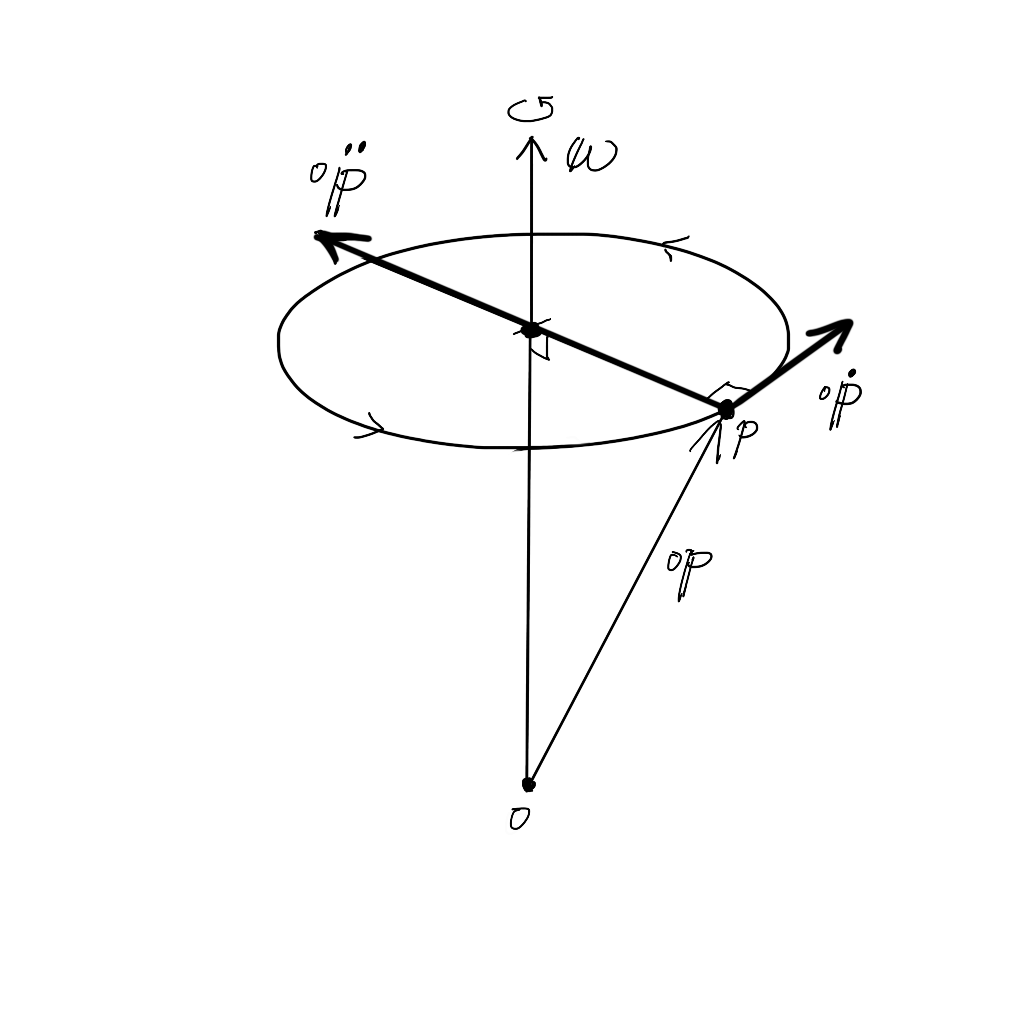
  等角速回転運動の加速度\( {}^{0}\ddot{\bf p} \)

• 大きさは\( \ddot{\theta} = 0 \)より、
  $$
  |{}^{0}{\ddot{\bf p}}| = \dot{\theta}^2|r|
  $$
  です。

7.3. 等角速回転運動のときの躍度

\( \ddot{\theta} = 0 \)、\({}^{0}\dot{\bf \omega} = {\bf 0}\)となるため、躍度は以下のようになります。

$$
{}^{0}{{\bf p}^{(3)}} = \ – \ {}^{0}{\bf \omega}^{2}\  {}^{0}{\bf \omega} \times {}^{0}{\bf p}
$$

• 方向は\( {}^{0}{\bf \omega} \times {}^{0}{\bf p} \)のマイナス定数倍なので、速度と平行で逆方向の向きになります。
• 大きさは
  $$ \begin{array}{rcl}
  | {}^{0}{{\bf p}^{(3)}} | &=& | {}^{0}{\bf \omega}^{2} | \left| {}^{0}{\bf \omega} \times {}^{0}{\bf p} \right| \\
  &=& |\dot{\theta}^{2}| |\dot{\theta}||r| \\
  &=& |\dot{\theta}^{3}| |r|
  \end{array}
  $$
  です。

 

 

8. まとめ(一つの回転軸まわりの回転運動における、質点の位置姿勢の速度、加速度、躍度)

8.1. ある点Pの回転運動

まとめます。

ある点Pの回転運動の速度\( {}^{0}{\dot{\bf p}} \)

$$
{}^{0}{\dot{\bf p}} = {}^{0}{\bf \omega} \times {}^{0}{\bf p}
$$

ある点Pの回転運動の加速度\( {}^{0}{\ddot{\bf p}} \)

$$
{}^{0}{\ddot{\bf p}} = {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf p} + {}^{0}{\bf \omega} \times \left( {}^{0}{\bf \omega} \times {}^{0}{\bf p} \right)
$$

ある点Pの回転運動の躍度\( {}^{0}{{\bf p}^{(3)}} \)

$$
{}^{0}{{\bf p}^{(3)}} = {}^{0}{\ddot{\bf \omega}} \times {}^{0}{\bf p} + 2{}^{0}{\dot{\bf \omega}} \times \left( {}^{0}{\bf \omega} \times {}^{0}{\bf p} \right)
+ {}^{0}{\bf \omega} \times \left( {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf p} \right )
\ – \ {}^{0}{\bf \omega}^{2}\  {}^{0}{\bf \omega} \times {}^{0}{\bf p}
$$

 

基底ベクトルの回転運動

冒頭に述べたとおり、
ある点Pのベクトル\( {}^{0}{\bf p} \)は、基底ベクトル\( {}^{0}{\bf x}_{{}^{0}{\bf e}_{x}}\), \( {}^{0}{\bf y}_{{}^{0}{\bf e}_{y}}\), \( {}^{0}{\bf z}_{{}^{0}{\bf e}_{z}}\)に置き直しても同じです。

基底ベクトルの回転運動の速度

$$ \begin{array}{rcl}
{}^{0}\dot{\bf x}_{{}^{0}{\bf e}_{x}} &=& {}^{0}{\bf \omega} \times {}^{0}{\bf x}_{{}^{0}{\bf e}_{x}} \\
{}^{0}\dot{\bf y}_{{}^{0}{\bf e}_{y}} &=& {}^{0}{\bf \omega} \times {}^{0}{\bf y}_{{}^{0}{\bf e}_{y}} \\
{}^{0}\dot{\bf z}_{{}^{0}{\bf e}_{z}} &=& {}^{0}{\bf \omega} \times {}^{0}{\bf z}_{{}^{0}{\bf e}_{z}}
\end{array}
$$

基底ベクトルの回転運動の加速度

$$ \begin{array}{rcl}
{}^{0}\ddot{\bf x}_{{}^{0}{\bf e}_{x}} &=& {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf x}_{{}^{0}{\bf e}_{x}} \
+ {}^{0}{\bf \omega} \times \left( {}^{0}{\bf \omega} \times {}^{0}{\bf x}_{{}^{0}{\bf e}_{x}} \right) \\
{}^{0}\ddot{\bf y}_{{}^{0}{\bf e}_{y}} &=& {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf y}_{{}^{0}{\bf e}_{y}} \
+ {}^{0}{\bf \omega} \times \left( {}^{0}{\bf \omega} \times {}^{0}{\bf y}_{{}^{0}{\bf e}_{y}} \right) \\
{}^{0}\ddot{\bf z}_{{}^{0}{\bf e}_{z}} &=& {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf z}_{{}^{0}{\bf e}_{z}} \
+ {}^{0}{\bf \omega} \times \left( {}^{0}{\bf \omega} \times {}^{0}{\bf z}_{{}^{0}{\bf e}_{z}} \right)
\end{array}
$$

基底ベクトルの回転運動の躍度

$$ \begin{array}{rcl}
{}^{0}{\bf x}_{{}^{0}{\bf e}_{x}}^{(3)} &=& {}^{0}\ddot{\bf \omega} \times {}^{0}{\bf x}_{{}^{0}{\bf e}_{x}}
+ 2{}^{0}{\dot{\bf \omega}} \times \left( {}^{0}{\bf \omega} \times {}^{0}{\bf x}_{{}^{0}{\bf e}_{x}} \right)
+ {}^{0}{\bf \omega} \times \left( {}^{0}\dot{\bf \omega} \times {}^{0}{\bf x}_{{}^{0}{\bf e}_{x}} \right )
\ – \ {}^{0}{\bf \omega}^{2}\  {}^{0}{\bf \omega} \times {}^{0}{\bf x}_{{}^{0}{\bf e}_{x}} \\
{}^{0}{\bf y}_{{}^{0}{\bf e}_{y}}^{(3)} &=& {}^{0}\ddot{\bf \omega} \times {}^{0}{\bf y}_{{}^{0}{\bf e}_{y}}
+ 2{}^{0}{\dot{\bf \omega}} \times \left( {}^{0}{\bf \omega} \times {}^{0}{\bf y}_{{}^{0}{\bf e}_{y}} \right)
+ {}^{0}{\bf \omega} \times \left( {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf y}_{{}^{0}{\bf e}_{y}} \right )
\ – \ {}^{0}{\bf \omega}^{2}\  {}^{0}{\bf \omega} \times {}^{0}{\bf y}_{{}^{0}{\bf e}_{y}} \\
{}^{0}{\bf x}_{{}^{0}{\bf e}_{x}}^{(3)} &=& {}^{0}\ddot{\bf \omega} \times {}^{0}{\bf z}_{{}^{0}{\bf e}_{z}}
+ 2{}^{0}{\dot{\bf \omega}} \times \left( {}^{0}{\bf \omega} \times {}^{0}{\bf z}_{{}^{0}{\bf e}_{z}} \right)
+ {}^{0}{\bf \omega} \times \left( {}^{0}\dot{\bf \omega} \times {}^{0}{\bf z}_{{}^{0}{\bf e}_{z}} \right )
\ – \ {}^{0}{\bf \omega}^{2}\  {}^{0}{\bf \omega} \times {}^{0}{\bf z}_{{}^{0}{\bf e}_{z}} \\
\end{array}
$$

8.3. 姿勢の回転運動

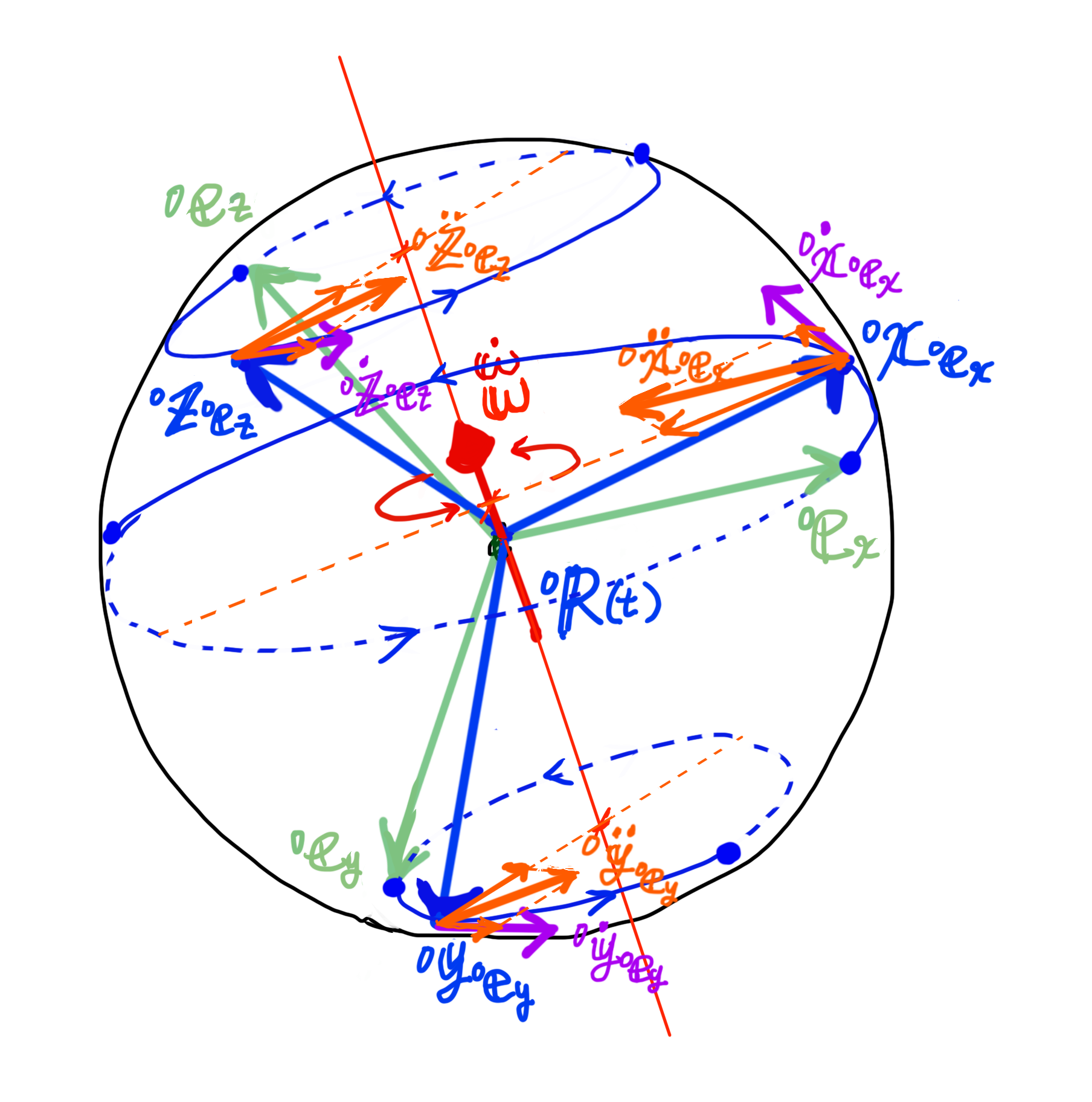
基底ベクトルの回転速度、加速度を図に表すとこんな感じでしょうか(イメージです)。

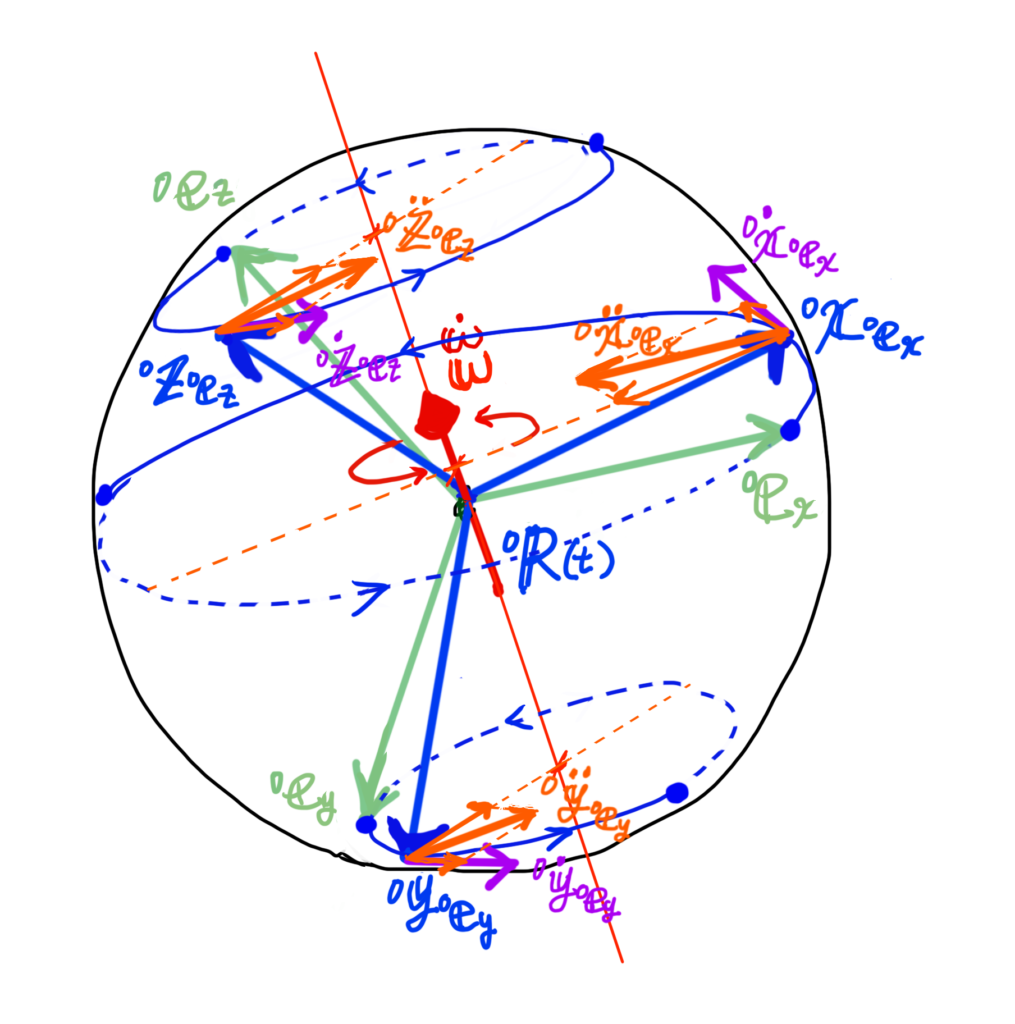
以前、剛体の運動(回転行列の速度とは)にて、
回転行列は、基底ベクトル\( {}^{0}{ \bf  e}_{x} \), \( {}^{0}{ \bf  e}_{y} \), \( {}^{0}{ \bf  e}_{z} \)が回転したベクトル\( {}^{0}{ \bf  x}_{ {}^{0}{ \bf  e}_{x} } \), \( {}^{0}{ \bf  y}_{ {}^{0}{ \bf  e}_{y} } \), \( {}^{0}{ \bf  z}_{ {}^{0}{ \bf  e}_{z} } \)により構成されるとノートしました。

$$
{}^{0}{ \bf R}(t) = \left[ \begin{array}{ccc}
{}^{0}{ \bf  x}_{ {}^{0}{ \bf  e}_{x} }  & {}^{0}{ \bf  y}_{ {}^{0}{ \bf  e}_{y} } & {}^{0}{ \bf  z}_{ {}^{0}{ \bf  e}_{z} }
\end{array} \right]
$$

また、回転行列\( {}^{0}{ \bf R}(t) \)は時刻\( t \)での姿勢を表しているとノートしました。

前述の基底ベクトルの速度、加速度の導出を踏まえると、
一つの回転軸まわりに回転する時の、姿勢の速度\( {}^{0}\dot{ \bf R}(t) \)、加速度\( {}^{0}\ddot{ \bf R}(t) \)、躍度\( {}^{0}{\bf R}^{(3)}(t) \)も同様に表すことができます。

姿勢の速度

$$
{}^{0}\dot{\bf R}(t) = {}^{0}{\bf \omega} \times {}^{0}{\bf R}(t)
$$

 

姿勢の加速度

$$
{}^{0}\ddot{\bf R}(t) = {}^{0}{\dot{\bf \omega}} \times {}^{0}{\bf R}(t) \
+ {}^{0}{\bf \omega} \times \left( {}^{0}{\bf \omega} \times {}^{0}{\bf R}(t) \right)
$$

 

姿勢の躍度

$$
{}^{0}{\bf R}^{(3)}(t) = {}^{0}\ddot{\bf \omega} \times {}^{0}{\bf R}(t)
+ 2{}^{0}{\dot{\bf \omega}} \times \left( {}^{0}{\bf \omega} \times {}^{0}{\bf R}(t) \right)
+ {}^{0}{\bf \omega} \times \left( {}^{0}\dot{\bf \omega} \times {}^{0}{\bf R}(t) \right )
\ – \ {}^{0}{\bf \omega}^{2}\  {}^{0}{\bf \omega} \times {}^{0}{\bf R}(t)
$$

 

 

 

ふぅ～。。

この辺は回転運動の話でよく出る話ですね。

記述の仕方はそれぞれ違うかと思われますが、角加速時と等角速時の両方ちゃんと書いておくと、

「もしこんな加速度で運動させるとき、位置、速度をどう設定して動作軌道をつくるか」

みたいなことを考えるとき役立つと思います。

 

以上です。