こんにちは。だいCです。
前回「剛体の回転行列の速度とは」で、姿勢の変化は基底ベクトルの移動を表していて、
基底ベクトルの移動の仕方は、回転角の変化\( \Delta \theta \)(\( \theta(t)の軌道計算 \))と回転軸\( \bf n \)に依存する、と書きました。
では、スタートとゴールの2つ姿勢が決まっていて、その間を1つの回転軸で回転移動するとき、間の姿勢はどうなるでしょうか?
回転軸\( \bf n \)はどのような値をとるのでしょうか…?
今回は2つの姿勢の間の姿勢、いわゆる姿勢の補間方法についてノートします。
1. 目的
2つの姿勢間を補間する方法を求める。
2. イメージ
前回、
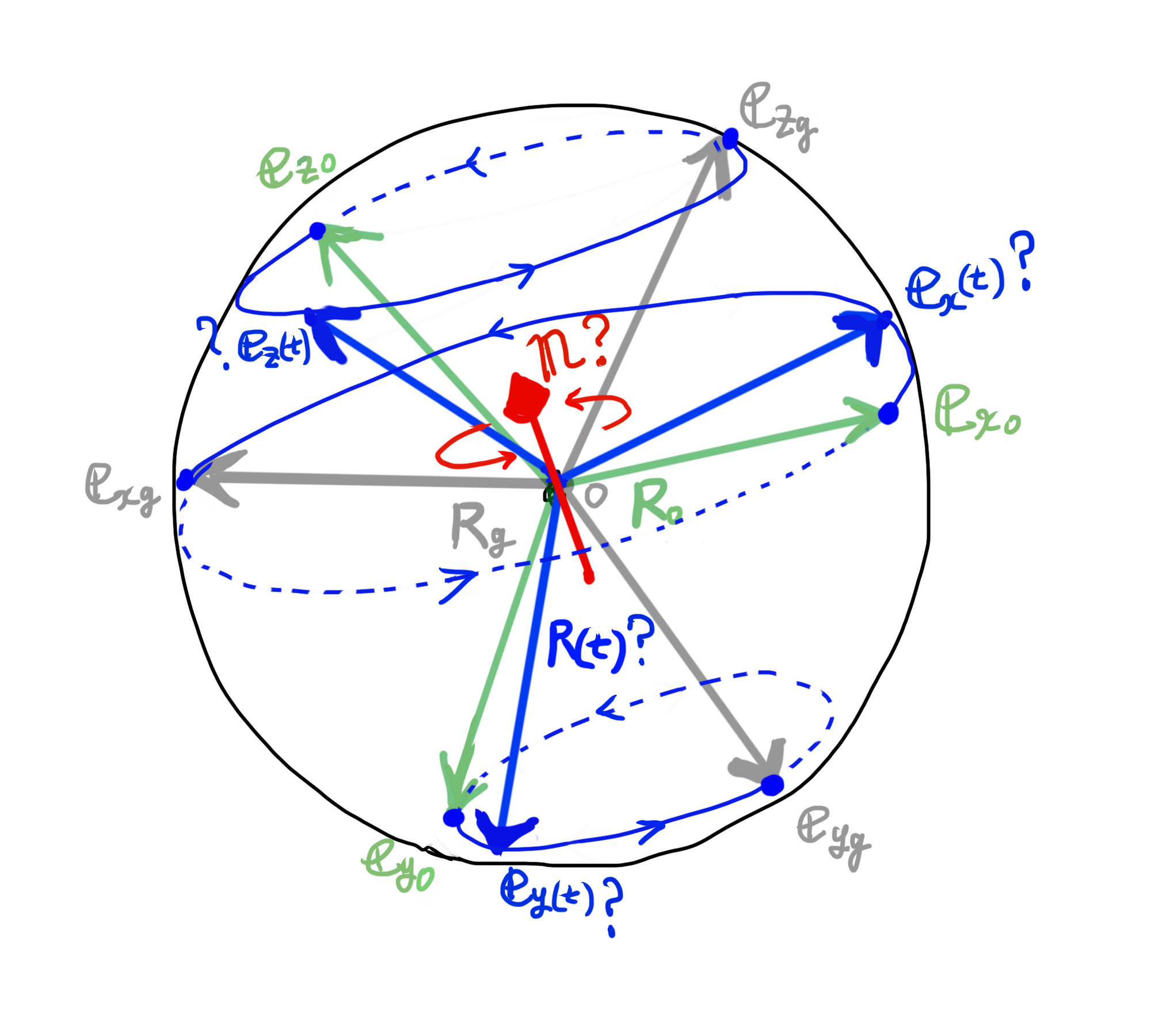
回転行列で表される姿勢の運動は、xyz軸で構成される正規直交基底の運動であり、xyz軸3本のベクトルは直交したまま球の表面を移動することをノートしました。
では、2つの姿勢間を移動するイメージの絵を描きます。
まず、最初異動する前の姿勢を以下に描きました。
球の表面に3点をとり、同じ球の中心からそれらの点に伸びる3軸が、互いに直交した基底ベクトル3本の組を姿勢として表現します。
よく座標系を表現するときこのような座標軸を描きますね。ここでは、姿勢を表す物体だと思ってください。
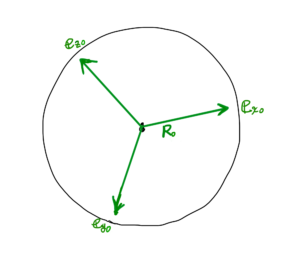
最初の姿勢を\( {\bf R}_0 \)とします。基底ベクトルは\( {\bf e}_{x0} \)、\( {\bf e}_{y0} \)、\( {\bf e}_{z0} \)とします。
この姿勢が点\( O \)を中心として回転し、ある時間経過後、ある姿勢に到達したとします。
到達後の姿勢を下の図ように描き足しました。
これを目標到達姿勢とよび、\( {\bf R}_{g}\)とします。基底ベクトルは\( {\bf e}_{xg} \)、\( {\bf e}_{yg} \)、\( {\bf e}_{zg} \)とします。
(下付き文字を目標=goalだから略してgとしましたが、終端=finishだから略してfと書くこともあります。ここではgとします。)
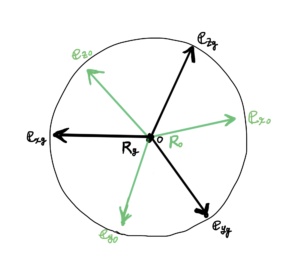
開始姿勢\( {\bf R}_0 \)と目標到達姿勢\( {\bf R}_{g} \)への回転移動は、
移動途中に複数の回転軸をとれば、ぐにゃぐにゃいろんな移動方法をとることができます。
ここでは、1つの回転軸だけとり、2つの姿勢間をその軸まわりにだけ回転移動することにします。
1つの回転軸のイメージを下の図のように描いてみます。
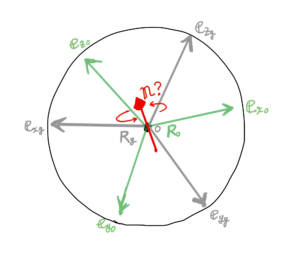
この1つの回転軸を\( \bf n \)とします。
2つの姿勢間を結ぶ1つの回転軸\( \bf n \)はどのようにして求められるでしょうか?
さらにこの回転軸\( \bf n \)で回転したときの、開始姿勢\( {\bf R}_0 \)と目標到達姿勢\( {\bf R}_{g} \)の間の姿勢\( {\bf R}(t) \)を以下のように描いてみました。
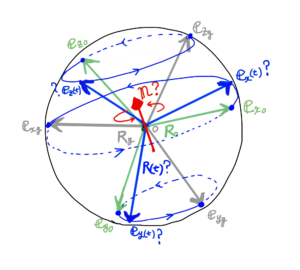
あいだの補間姿勢について、
開始姿勢から移動開始する時刻を0とし、到達姿勢に到達する時刻を1として說明することがあります。
なぜ0から1にするかというと、軌道補間の実装上、話がラクだからです。
開始時刻、到達時刻のとり方なんて無限にありますが、例えば、開始時刻を\(t_0\)、目標到達時刻を\(t_g\)とし、
その間の時刻\( t \)を、たとえば下式のようにパラメータ\( s \)に置き換えてやれば、
$$
s(t) = \frac{t – t_0}{t_g – t_0}
$$
範囲\( [t_0, t_g] \)間の移動を\( [0, 1] \)間の移動、つまり開始点と目標点の間の内分比パラメータの時間変化とすることができるのです。
軌道補間計算を実装するとき、余計な定数の入力文字を考えなくていいのでラクチンです。
これは軌道補間の教科書や論文でもよく見られ、もはや当たり前のように補間を媒介する変数\(s\)は0~1として説明されることもあります。
以降、自分もこのように、\(s\)を補間時刻\(s \in [0, 1]\)として話をすすめることもあるので、ご注意ください。
では話を戻して、時刻\( t \)のときの補間姿勢\( {\bf R}(s(t)) \)はどのようにして求まるでしょうか?
3. 2つの姿勢間の補間方法
ここで、回転運動を作用する回転行列\( {\bf R}_{0 \rightarrow g} \)と仮において、
開始姿勢\( {\bf R}_{0} \)が、回転運動\( {\bf R}_{0 \rightarrow g} \)の作用によって、目標到達姿勢\( {\bf R}_{g} \)に到達したと考えます。
$$
{\bf R}_{g} = {\bf R}_{0 \rightarrow g} {\bf R}_{0}
$$
この回転行列\( {\bf R}_{0 \rightarrow g} \)は以下のように求まります。
$$
{\bf R}_{0 \rightarrow g} := {\bf R}_{g}{\bf R}^{\rm T}_{0}
$$
この回転行列\( {\bf R}_{0 \rightarrow g} \)が、先程イメージで描いた回転軸\( \bf n \)まわりに \( \theta(s(t_0))(=\theta_0=0) \) から\( \theta(s(t_g))(=\theta_g) \)へ回転する回転運動全体を表しています。
回転行列\( {\bf R}_{0 \rightarrow g} \)にある回転角\( \theta \) ( \( \theta_0(=0) \le \theta \le \theta_g \) ) を与えると、その回転運動のあいだの1つの姿勢への変換作用\( {\bf R}_{0 \rightarrow g}( \theta ) \)を得ることできます。
回転角\( \theta \)は、入力\( s(t) \)の関数とします。
今回は、\( \theta \)と\( s(t) \)の関係は置いておいて、\( s(t) \)により求まった回転角\( \theta \)を入力として与えることができるとします。
よって、先程まで\( {\bf R}(s(t)) \)と表していた回転行列の姿勢は、開始姿勢\( {\bf R}_{0} \)に対し直接の入力\( \theta \)の関数が作用した姿勢、\( {\bf R}_{0 \rightarrow g}(\theta) {\bf R}_{0} \)と表わせます。
\( \theta \)を入力とすると、上式の\( {\bf R}_{0 \rightarrow g} \)から、\( {\bf R}_{0 \rightarrow g}( \theta ) \)がどのような値になるか求めます。
剛体の運動(回転行列と角軸)での内容を使います。
上式で求めた回転行列\( \bf R_{0 \rightarrow g} \)の要素を以下のように置くと、
$$
{\bf R}_{0 \rightarrow g} = \left[ \begin{array}{ccc}
r_{11} & r_{12} & r_{13} \\
r_{21} & r_{22} & r_{23} \\
r_{31} & r_{32} & r_{33}
\end{array} \right]
$$
回転軸\( \bf n \)は以下のように求まるのでした。これが1つの回転軸\( \bf n \)を求める方法の解答です。
$$
{\bf n}_{\rm id} := \left[ \begin{array}{c}
r_{32} – r_{23}\\
r_{13} – r_{31}\\
r_{21} – r_{12}
\end{array} \right]
$$
$${\bf n} := \frac{ {\bf n}_{\rm id} }{ \| {\bf n}_{\rm id} \| }$$
開始姿勢\( {\bf R}_{0} \)の要素を以下のように書くと、
$$
{\bf R}_{0} = \left[ \begin{array}{ccc}
r_{0\_11} & r_{0\_12} & r_{0\_13} \\
r_{0\_21} & r_{0\_22} & r_{0\_23} \\
r_{0\_31} & r_{0\_32} & r_{0\_33}
\end{array} \right]
$$
このときの回転角\( \theta_0 \)は、以下のように求まるのでした。
$$
\theta_0 = { \rm atan2 } \left( \frac{1}{2} \| {\bf n}_{\rm id} \|, \frac{r_{0\_11} + r_{0\_22} + r_{0\_33}-1}{2} \right)
$$
同様にして、終端姿勢の回転角\( \theta_g \)も求まります。
補間姿勢の入力回転角\( \theta\)は、\( \theta_0 \)と\( \theta_g \)を元にした軌道補間計算より、予め\(s\)の関数として求めておきます。
ロドリゲスの公式より、入力\( \theta \)のときの回転軸\( {\bf n} \)まわりの姿勢\( {\bf R}(\theta) \)として、補間姿勢\( {\bf R}_{0 \rightarrow g}(t)={\bf R}_{0 \rightarrow g}(\theta) \)が求まります。
$$ {\bf R}_{0 \rightarrow g}(\theta) := {\bf I} + {\rm sin}\theta {\bf[ n\times]} + (1 – {\rm cos}\theta) {\bf[ n\times]}^2 $$
( \( \bf I\)は単位行列、\( \bf[ n\times] \)は\( {\bf n} \)による外積行列 )
最終的に回転作用\( {\bf R}_{0 \rightarrow g}(\theta) \)によって姿勢\( {\bf R}_{0} \)から移動した姿勢\( {\bf R}(s(t)) \)を求めます。
$$
{\bf R}(s(t)) = {\bf R}_{0 \rightarrow g}(\theta) {\bf R}_{0}
$$
以上で、2つ目の問題の解答である、補間姿勢\( {\bf R}(s(t)) \)を求めることできました。
4. まとめ
以上をまとめます。
入力
- 開始姿勢\( {\bf R}_{0} \)
- 到達姿勢\( {\bf R}_{g} \)
- 開始時刻\( t_0 \)
- 終端時刻\( t_g \)
- 時刻\( t \)
出力
- 時刻\( t \)のときの補間姿勢\( {\bf R}(s(t)) \)
アルゴリズム
- 開始姿勢\( {\bf R}_{0} \)と到達姿勢\( {\bf R}_{g} \)より、2姿勢間の回転運動の作用を表す\( {\bf R}_{0 \rightarrow g} \)を求める。
$$
{\bf R}_{0 \rightarrow g} := {\bf R}_{g}{\bf R}^{\rm T}_{0}
$$$$
\left(
{\bf R}_{0} = \left[ \begin{array}{ccc}
r_{0\_11} & r_{0\_12} & r_{0\_13} \\
r_{0\_21} & r_{0\_22} & r_{0\_23} \\
r_{0\_31} & r_{0\_32} & r_{0\_33}
\end{array} \right], \\
{\bf R}_{g} = \left[ \begin{array}{ccc}
r_{g\_11} & r_{g\_12} & r_{g\_13} \\
r_{g\_21} & r_{g\_22} & r_{g\_23} \\
r_{g\_31} & r_{g\_32} & r_{g\_33}
\end{array} \right], \\
{\bf R}_{0 \rightarrow g} = \left[ \begin{array}{ccc}
r_{11} & r_{12} & r_{13} \\
r_{21} & r_{22} & r_{23} \\
r_{31} & r_{32} & r_{33}
\end{array} \right]
\right)
$$ - 回転行列\( {\bf R}_{0 \rightarrow g} \)より、回転軸\({\bf n}\)を求める。
$$
{\bf n}_{\rm id} := \left[ \begin{array}{c}
r_{32} – r_{23} \\
r_{13} – r_{31} \\
r_{21} – r_{12}
\end{array} \right]
$$$${\bf n} := \frac{ {\bf n}_{\rm id} }{ \| {\bf n}_{\rm id} \| }$$
- 開始回転角\( \theta_{0} \)を求める。
$$ \theta_0 := { \rm atan2 } \left( \frac{1}{2} \| {\bf n}_{\rm id} \|, \frac{r_{0\_11} + r_{0\_22} + r_{0\_33}-1}{2} \right) $$ - 終端回転角\( \theta_{g} \)を求める。
$$ \theta_g := { \rm atan2 } \left( \frac{1}{2} \| {\bf n}_{\rm id} \|, \frac{r_{g\_11} + r_{g\_22} + r_{g\_33}-1}{2} \right) $$ - 軌道補間計算により時刻 \( t \)のときの回転角\( \theta(s(t)) \)を求める。
ここでは軌道補間計算の方法は省略。入出力だけ示す。
・入力:開始時刻\(t_0\)、終端時刻\( t_g \)、時刻\( t \)、開始回転角\( \theta_0 \)、終端回転角\( \theta_{g} \)
・出力:時刻\(t\)のときの回転角\( \theta(s(t)) \) . - ロドリゲスの公式より、回転角\( \theta \)のときの回転作用\( {\bf R}_{0 \rightarrow g}(\theta) \)を求める。
$$ {\bf R}_{0 \rightarrow g}(\theta) := {\bf I} + {\rm sin}\theta {\bf[ n\times]} + (1 – {\rm cos}\theta) {\bf[ n\times]}^2 $$ - 出力\( {\bf R}(s(t)) := {\bf R}_{0 \rightarrow g}(\theta) {\bf R}_{0} \)を得る。
以上です。