こんにちは。
だいCです。
このブログはノート代わりに使っています。
今回は回転&並進についてノートします。
1. 目的
1つの回転軸まわりの回転と並進が複合した運動における、
質点の位置姿勢の速度・加速度を求める
2. 回転と並進が複合した運動を考える場面
日常だとあまり意識しないかもしれませんが、例えば
- 乗り物でカーブしながら車線変更するときや、
- 北半球の気象衛星画像に写った低気圧が反時計回りになっているのを目にしたとき、
- その他腰を回しながら腕を伸縮するような身体動作をしているとき
など、回転と並進による運動を体感しているみたいですね~。。全然気にしたことなかったですが。
ロボットでも、このような回転&並進による運動の影響は、ユーザーレベルで気にすることはほとんどないと思います。
しかし、ロボットの性能評価や動作設計をおこなう側では、例えば、
- 複数ある関節軸を同時に動かした時、各関節軸にかかる慣性負荷はどれくらいか
- 手先に液体等速度や加速度に影響を受ける物体を持たせて運ぶ時、回転と並進を伴う場合、どのような方向に動かせばよいか
などなどモデル化・定式化を考える場面で、さり気なく出てきます。
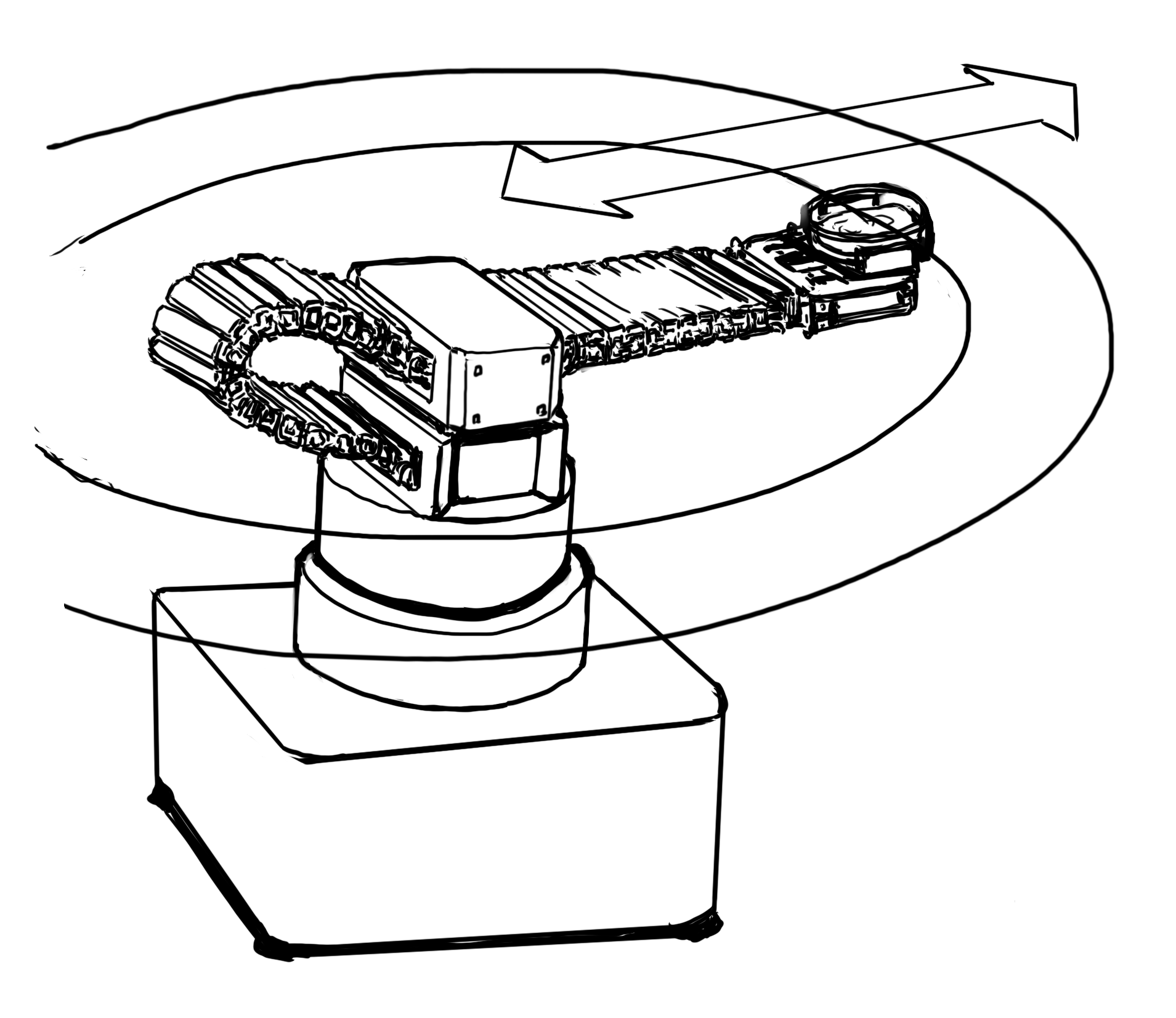
特に、下の図のようなPolar Robot(極座標型)とよばれる類のロボットは、回転と並進がわかりやすく組み合わされています。
ということで、回転と並進が組み合わさると、どのような速度・加速度をもつのか定式化してみましょう。
3. 前提
回転している軸、ここでは軸に限らず回転しているもの全般を指すように、回転系と言っておきましょうか。
回転系の上で、並進運動している座標系に働く速度と加速度を出力とします。
- 基準座標系を\( \Sigma_{0} \)、回転1と一緒に回る座標系を\( \Sigma_{1} \)、伸縮と一緒に回る座標系を\( \Sigma_{2} \)とします。
- 入力1:基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{1} \)の位置\( {}^{0}{\bf p}_{1} \)(一定)
- 入力2:基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{1} \)の姿勢\( {}^{0}{\bf R}_{1} \)
- 入力3:基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{1} \)の角速度ベクトル\( {}^{0}{\bf \omega}_{1} \) ( 回転軸\({}^{0}{\bf n}_{1} \), 角速度\(\dot{\theta_1}\) )
- 入力4:基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{1} \)の角加速度ベクトル\( {}^{0}\dot{\bf \omega}_{1} \) ( 回転軸\({}^{0}{\bf n}_{1} \), 角速度\(\ddot{\theta_1}\) )
- 入力5:座標系\( \Sigma_{1} \)から見た座標系\( \Sigma_{2} \)の位置\( {}^{1}{\bf p}_{2} \)
- 入力6:座標系\( \Sigma_{1} \)から見た座標系\( \Sigma_{2} \)の姿勢\( {}^{1}{\bf R}_{2} \)(一定)
- 入力7:座標系\( \Sigma_{1} \)から見た座標系\( \Sigma_{2} \)の並進速度\( {}^{1}{\bf \dot p}_{2} \)
- 入力8:座標系\( \Sigma_{1} \)から見た座標系\( \Sigma_{2} \)の並進加速度\( {}^{1}{\bf \ddot p}_{2} \)
- 入力9:座標系\( \Sigma_{2} \)から見た、座標系\( \Sigma_{2} \)と一緒に伸縮する点Pの位置ベクトル\( {}^{2}{\bf p}_{A} \)(一定)
- 出力1:基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の角速度ベクトル\( {}^{0}{\bf \omega}_{2} \)
- 出力2:基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の位置・姿勢の速度\( {}^{0}\dot{\bf p}_{2} \)、\( {}^{0}\dot{\bf R}_{2} \)
- 出力3:基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の角加速度ベクトル\( {}^{0}\dot{\bf \omega}_{2} \)
- 出力4:基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の位置・姿勢の加速度\( {}^{0}\ddot{\bf p}_{2} \)、\( {}^{0}\ddot{\bf R}_{2} \)
- 回転と伸縮の効果のみ注目したいので重力加速度を無視します。
4. 回転系上での伸縮における位置・姿勢の速度と加速度
座標系\(\Sigma_{0} \)基準の座標系\(\Sigma_{2} \)の位置\( {}^{0}{\bf p}_{2} \)は、入力\( {}^{0}{\bf p}_{1} \)、\( {}^{0}{\bf R}_{1} \)、\( {}^{1}{\bf p}_{2} \)を用いて以下のように求まります。
$$ \begin{array}{rcl}
{}^{0}{\bf p}_{2} &=& {}^{0}{\bf p}_{1} + {}^{0}{\bf p}_{1 \rightarrow 2} \\
&=& {}^{0}{\bf p}_{1} + {}^{0}{\bf R}_{1}{}^{1}{\bf p}_{2}
\end{array}
$$
座標系\(\Sigma_{0} \)基準の座標系\(\Sigma_{2} \)の姿勢\( {}^{0}{\bf R}_{2} \)は、入力\( {}^{0}{\bf R}_{1} \)、\( {}^{1}{\bf R}_{2} \)を用いて以下のように求まります。
$$ \begin{array}{rcl}
{}^{0}{\bf R}_{2} = {}^{0}{\bf R}_{1} {}^{1}{\bf R}_{2}
\end{array}
$$
以降、この\( {}^{0}{\bf p}_{2} \)、\( {}^{0}{\bf R}_{2} \)の式を用います。
\( {}^{0}{\bf p}_{2} \)を微分して、
入力\( {}^{0}{\bf R}_{1} \)、\( {}^{0}{\bf \omega}_{1} \)、\( {}^{1}{\bf p}_{2} \)、\( {}^{1}{\bf \dot p}_{2} \)を用い、座標系\(\Sigma_{0} \)基準の座標系\(\Sigma_{2} \)の速度\( {}^{0}{\bf \dot p}_{2} \)を表すと以下のようになります。ただし、\( {}^{0}{\bf p}_{1} \)が一定値であるため、その微分値\( {}^{0}{\bf \dot p}_{1} \)は0になります。
$$
\begin{array}{rcl}
{}^{0}{\bf \dot p}_{2} &=& {}^{0}{\bf \dot p}_{1} + {}^{0}{\bf \dot p}_{1 \rightarrow 2} \\
&=& 0 + \frac{\rm d}{\rm dt} \left( {}^{0}{\bf R}_{1}{}^{1}{\bf p}_{2} \right) \\
&=& {}^{0}{\bf \dot R}_{1} {}^{1}{\bf p}_{2} + {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \\
&=& [{}^{0}{\omega}_{1} \times] {}^{0}{\bf R}_{1} {}^{1}{\bf p}_{2} + {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \\
&=& {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf p}_{2} + {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2}
\end{array}
$$
座標系\( \Sigma_{0} \)基準で見た回転する座標系\( \Sigma_{2} \)の姿勢\( {}^{0}{\bf R}_{2} \)の速度\( {}^{0}{\bf \dot R}_{2} \)は、入力\( {}^{0}{\bf R}_{1} \)、\( {}^{1}{\bf R}_{2} \)との関係から微分して以下のように求まります。ただし、\( {}^{1}{\bf R}_{2} \)が一定値であるため、その微分値\( {}^{1}{\dot{\bf R}}_{2} \)は0になります。
$$ \begin{array}{rcl}
{}^{0}\dot{\bf R}_{2} &=& \frac{\rm d}{\rm dt} \left( {}^{0}{\bf R}_{1} {}^{1}{\bf R}_{2} \right) \\
&=& {}^{0}{\dot{\bf R}}_{1} {}^{1}{\bf R}_{2} + {}^{0}{\bf R}_{1} {}^{1}{\dot{\bf R}}_{2} \\
&=& [{}^{0}{\omega}_{1} \times] {}^{0}{\bf R}_{1} {}^{1}{\bf R}_{2} + 0 \\
&=& {}^{0}{\omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf R}_{2} \\
&=& {}^{0}{\omega}_{1} \times {}^{0}{\bf R}_{2}
\end{array}
$$
剛体の運動(回転運動の速度・加速度・躍度)でやったように、
速度を微分することで、点の位置・姿勢の加速度を求めます。
座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の位置の並進加速度は以下のようになります。
$$ \begin{array}{rcl}
{}^{0}\ddot{\bf p}_{2} &=& \
\frac{\rm d}{\rm dt} \left( {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf p}_{2} \
+ {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \right) \\
&=& {}^{0}{\bf \dot \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf p}_{2} \
+ {}^{0}{\bf \omega}_{1} \times \frac{\rm d}{\rm dt} \left( {}^{0}{\bf R}_{1} {}^{1}{\bf p}_{2} \right) \
+ {}^{0}{\bf \dot R}_{1} {}^{1}{\bf \dot p}_{2} + {}^{0}{\bf R}_{1} {}^{1}{\bf \ddot p}_{2} \\
&=& {}^{0}{\bf \dot \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf p}_{2} \
+ {}^{0}{\bf \omega}_{1} \times \left( {}^{0}{\bf \dot R}_{1} {}^{1}{\bf p}_{2} + {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \right) \
+ [{}^{0}{\bf \omega}_{1} \times ] {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} + {}^{0}{\bf R}_{1} {}^{1}{\bf \ddot p}_{2} \\
&=& {}^{0}{\bf \dot \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf p}_{2} \
+ {}^{0}{\bf \omega}_{1} \
\times \left( [{}^{0}{\bf \omega}_{1} \times ] {}^{0}{\bf R}_{1} {}^{1}{\bf p}_{2} + {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \right) \
+ [{}^{0}{\bf \omega}_{1} \times ] {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} + {}^{0}{\bf R}_{1} {}^{1}{\bf \ddot p}_{2} \\
&=& {}^{0}{\bf \dot \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf p}_{2} \
+ {}^{0}{\bf \omega}_{1} \times \left( {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf p}_{2} \right) \
+ {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \
+ {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} + {}^{0}{\bf R}_{1} {}^{1}{\bf \ddot p}_{2} \\
&=& {}^{0}{\bf \dot \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf p}_{2} \
+ {}^{0}{\bf \omega}_{1} \times \left( {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf p}_{2} \right) \
+ 2 {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \
+ {}^{0}{\bf R}_{1} {}^{1}{\bf \ddot p}_{2} \\
\end{array}
$$
この式のうち、ほとんどの項がこれまでノートした話に出てきていますね。
右辺第一項目は、座標系\(\Sigma_{0}\)から見た座標系\( \Sigma_{2} \)の、回転系の回転方向(接線方向)へ向かう接線加速度、
右辺第二項目は、座標系\(\Sigma_{0}\)から見た座標系\( \Sigma_{2} \)の、回転系の回転軸へ向かう求心加速度になります。
右辺第三項目は、今回初めて出てきます。一体どんな大きさと方向でしょうか、あとで說明します。
右辺第四項目は、座標系\(\Sigma_{0}\)から見た座標系\( \Sigma_{2} \)の、並進運動の加速度です。
一定角速度で回転し、一定並進速度で移動しているとき、第一項の角加速度、第四項の並進加速度は0になりますが、第二項の求心加速度と第三項の加速度は残ります。
また、座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の姿勢の加速度は、以下のようになります。
$$ \begin{array}{rcl}
{}^{0}\ddot{\bf R}_{2} &=& \frac{\rm d}{\rm dt} \left( {}^{0}{\omega}_{1} \times {}^{0}{\bf R}_{2} \right) \\
&=& {}^{0}{\dot \omega}_{1} \times {}^{0}{\bf R}_{2} + {}^{0}{\omega}_{1} \times {}^{0}{\bf \dot R}_{2} \\
&=& {}^{0}{\dot \omega}_{1} \times {}^{0}{\bf R}_{2} + \
{}^{0}{\omega}_{1} \times \left( {}^{0}{\omega}_{1} \times {}^{0}{\bf R}_{2} \right) \\
\end{array}
$$
この式は、同じく剛体の運動(回転運動の速度、加速度、躍度)でまとめたものと同じです。
さて、今回の主役である座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の、位置の加速度\( {}^{0}\ddot{\bf p}_{2} \)の式に現れた
第三項目
$$
2 {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2}
$$
が、一体どのような加速度なのか見てみましょう。
\( {}^{0}{\bf \omega}_{1} \)は、座標系\( \Sigma_{0} \)から見ると回っている座標系\( \Sigma_{1} \)の、回転系の角速度ベクトルです。
その大きさは角速度\( \dot \theta \)、方向は回転軸\({}^{0}{\bf n}_{1} \)方向を指しています。
\( {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \)は、座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の、並進速度方向です。その点での移動方向ですね。
この二つの外積ということは、外積の性質上、両者に垂直な方向、
すなわち回転軸と並進移動方向の両者に垂直な方向に働く加速度になります。
その加速度の方向を、図を交えて具体的に見てみましょう。
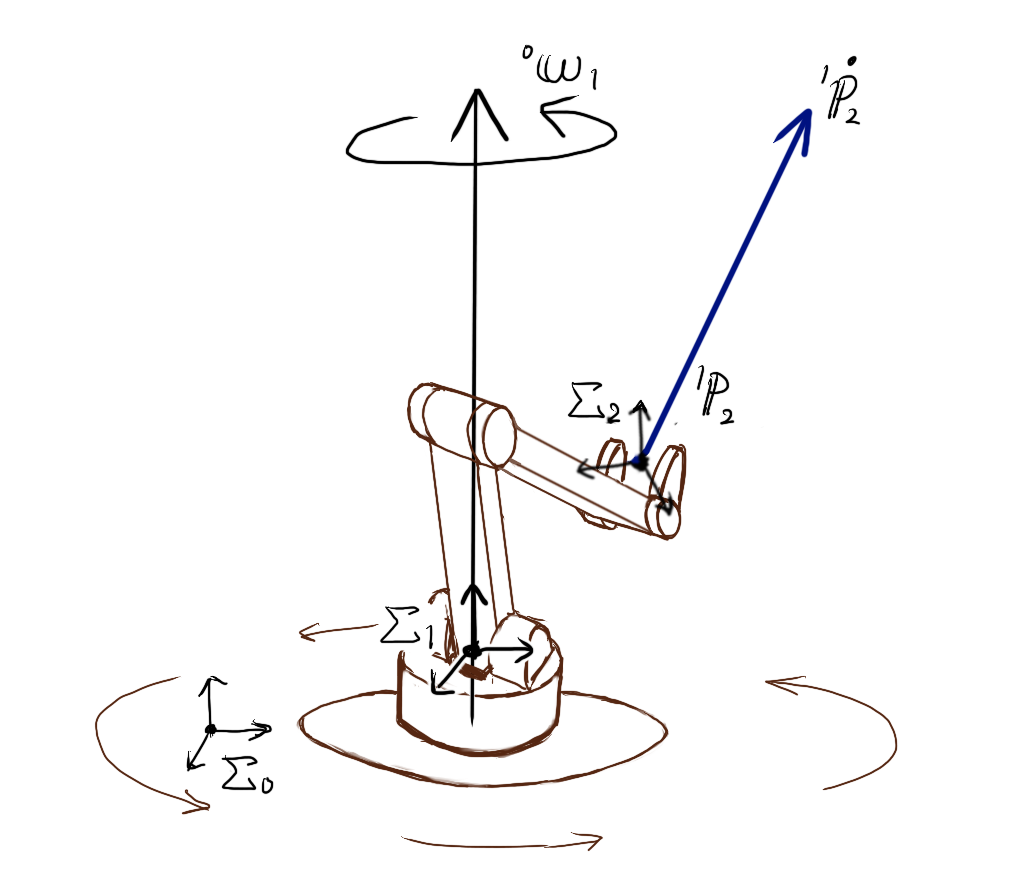
環境に固定された基準座標系\( \Sigma_{0} \)から見て、ヨー軸回転しているロボットの回転座標系\( \Sigma_{1} \)があります。
その回転座標系\( \Sigma_{1} \)上で、姿勢はそのままで、位置だけ並進移動している手先座標系\( \Sigma_{2} \)があるとします。
基準座標系\( \Sigma_{0} \)から見た回転座標系\( \Sigma_{1} \)の、姿勢は\( {}^{0}{\bf R}_{1} \)、回転速度ベクトルは\( {}^{0}{\bf \omega}_{1} \)、
座標系\( \Sigma_{1} \)から見た手先の座標系\( \Sigma_{2} \)の、位置は\( {}^{1}{\bf p}_{2} \)、並進速度のベクトルは\( {}^{1}{\bf \dot p}_{2} \)です。
上記の図では、基準座標系\( \Sigma_{0} \)の位置が、回転座標系\( \Sigma_{1} \)からずれた場所に描いちゃっていますが、両者の位置関係はとりあえず無視してください。
基準座標系\( \Sigma_{0} \)から見ると、手先の並進速度ベクトルは\( {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \)となります。
並進速度ベクトル\( {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \)を分解すると、回転速度ベクトル\( {}^{0}{\bf \omega}_{1} \)(回転軸)に平行な成分と、回転軸に垂直な面上に射影された方向成分に分解できます。
回転速度ベクトル\( {}^{0}{\bf \omega}_{1} \)と並進速度ベクトル\( {}^{1}{\bf \dot p}_{2} \)の外積 \( 2 {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \) を、この分解した成分で考えると、回転軸に平行な成分との外積は0になります。そのため、並進速度ベクトルのうち、回転軸に垂直な面上に射影された方向だけ残ります。この残った射影成分を以下のように図示します。
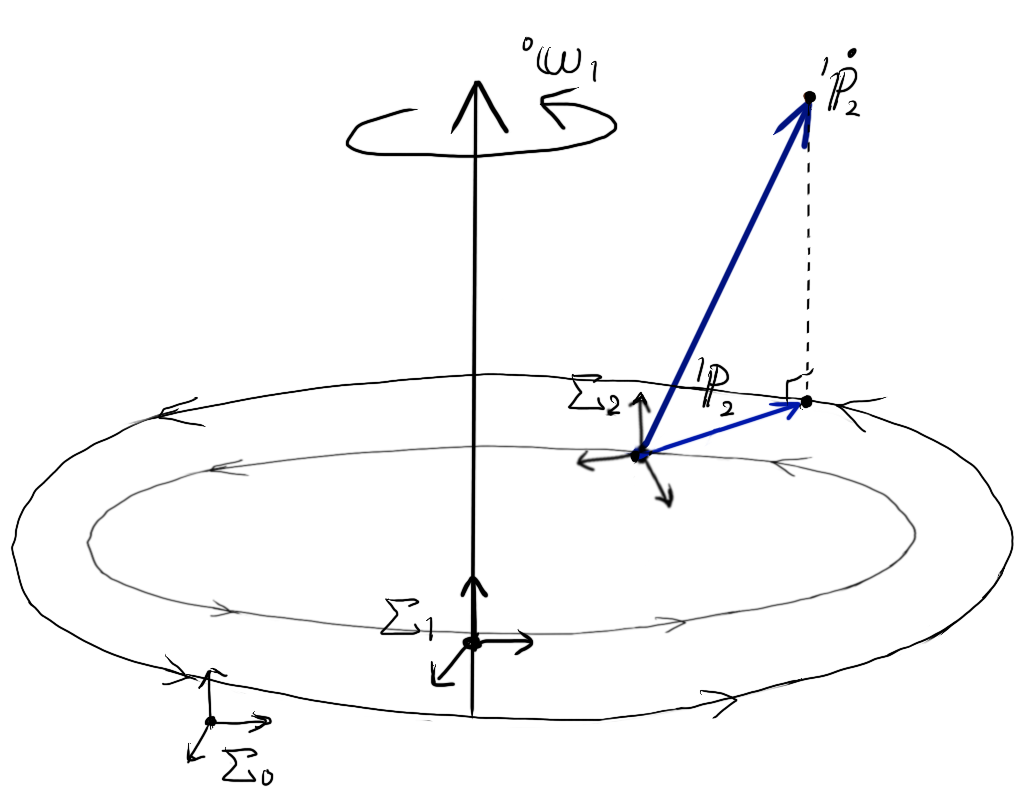
並進速度ベクトル\( {}^{1}{\bf \dot p}_{2} \)の射影成分はベクトルなので、大きさと方向さえ同じならば図のどこに平行移動してもいいので、同一平面上の回転速度ベクトル\( {}^{0}{\bf \omega}_{1} \)(回転軸)へと開始点を平行移動させてみます。
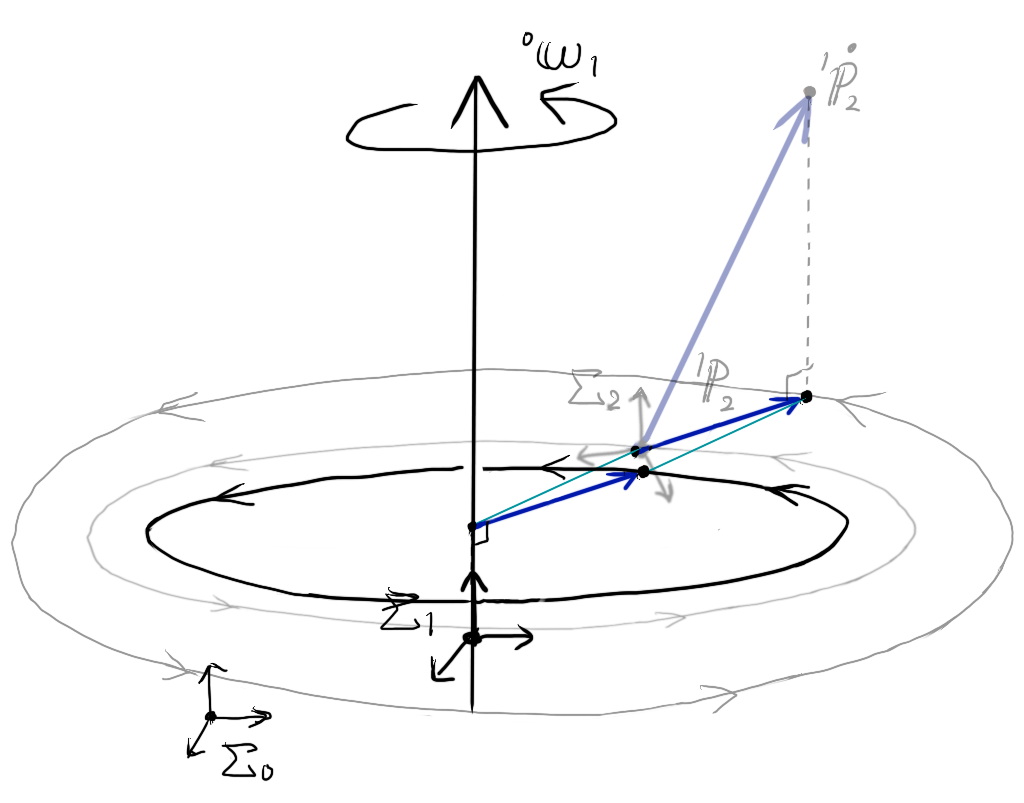
この図に外積 \( 2 {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \) を図示してみます。回転速度ベクトル\( {}^{0}{\bf \omega}_{1} \)と並進速度ベクトル\( {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \)の両方に垂直なので、平行移動した並進速度ベクトルが描く回転円に接する方向に、外積のベクトル(赤線)を描けることがわかります。
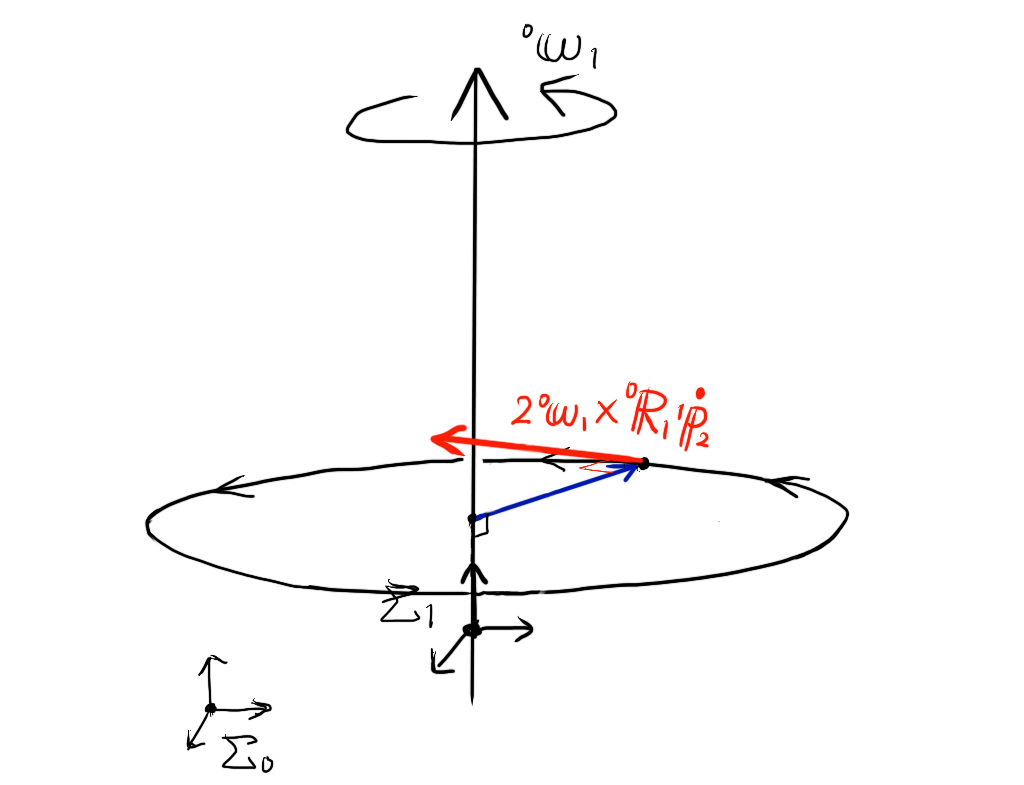
外積 \( 2 {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \) を、開始点を手先位置\( {}^{1}{\bf p}_{2} \)と共に平行移動して戻してやると、以下の図のようになります。
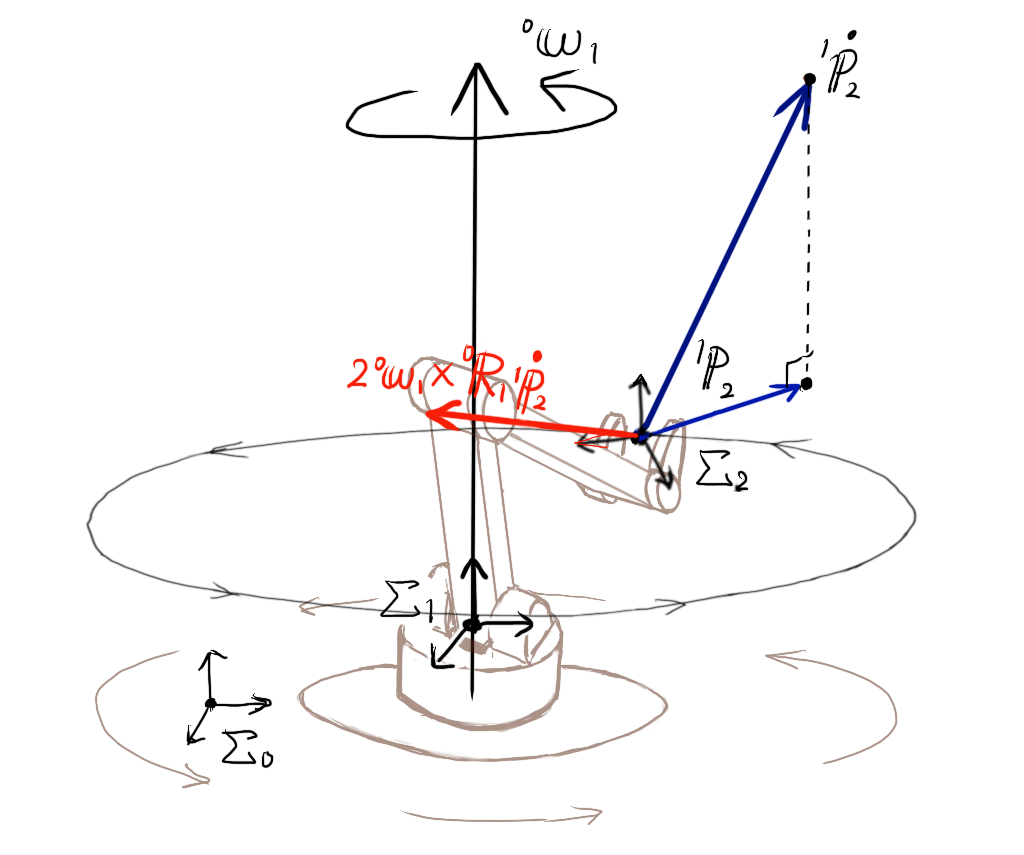
以上の図から分かるように、加速度 \( 2 {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \) は、常に並進速度ベクトル\({\bf \dot p}_{2} \)を、回転軸に垂直な平面上へ射影し、さらにその射影方向に対し垂直にとった方向にはたらくことを表しています。
注意が必要なのは、平行移動したことから分かるように、加速度 \( 2 {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \) は、位置\( {}^{1} {\bf p}_{2} \)(座標系\(\Sigma_{0}\)における\( {}^{0} {\bf p}_{1 \rightarrow 2} \))から、\(\Sigma_{1}\)の回転円接線方向に向いているわけではないということです。
あくまで並進速度ベクトル \( {}^{1}{\bf \dot p}_{2} \) に垂直な方向であるということを誤解してはいけません。
この加速度 \( 2 {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \) は、回転系上で並進移動するときに必要になります。逆に手先座標系\(\Sigma_{2} \)から見ると、逆向きの方向の加速度 \( – 2 {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \) がはたらいているように見えます。
この手先座標系\(\Sigma_{2} \)から見た加速度が、質点に対し働くみかけの力を、コリオリの力(Coriolis force)と呼ぶそうです。
この慣性力は、ガスパール=ギュスターヴ・コリオリ(Gaspard-Gustave Coriolis 1792年5月21日 – 1843年9月19日)さんが正式に導出したので、彼の名にちなんでコリオリの力と呼ばれるようになったそうです。物理法則に自分の名前が付くってすごいですよね。
5. まとめ(回転系上での伸縮における位置・姿勢の速度と加速度)
まとめます。
ステップ1. 座標系\(\Sigma_{0} \)基準の座標系\(\Sigma_{2} \)の位置\( {}^{0}{\bf p}_{2} \)、姿勢\( {}^{0}{\bf R}_{2} \)
座標系\(\Sigma_{0} \)基準の座標系\(\Sigma_{2} \)の位置\( {}^{0}{\bf p}_{2} \)を、入力\( {}^{0}{\bf p}_{1} \)、\( {}^{0}{\bf R}_{1} \)、\( {}^{1}{\bf p}_{2} \)を用いて以下のように求めます。
$$ \begin{array}{rcl}
{}^{0}{\bf p}_{2} = {}^{0}{\bf p}_{1} + {}^{0}{\bf R}_{1}{}^{1}{\bf p}_{2} \\
\end{array}
$$
座標系\(\Sigma_{0} \)基準の座標系\(\Sigma_{2} \)の姿勢\( {}^{0}{\bf R}_{2} \)を、入力\( {}^{0}{\bf R}_{1} \)、\( {}^{1}{\bf R}_{2} \)を用いて以下のように求めます。
$$ \begin{array}{rcl}
{}^{0}{\bf R}_{2} = {}^{0}{\bf R}_{1} {}^{1}{\bf R}_{2}
\end{array}
$$
ステップ2. (出力1) 座標系\(\Sigma_{0} \)基準で見た座標系\( \Sigma_{2} \)の位置・姿勢の速度\( {}^{0}\dot{\bf p}_{2} \)、\( {}^{0}\dot{\bf R}_{2} \)
座標系\(\Sigma_{0} \)基準で見た座標系\( \Sigma_{2}\)の位置・姿勢の速度\( {}^{0}\dot{\bf p}_{2} \)、\( {}^{0}\dot{\bf R}_{2} \)を、入力\( {}^{0}{\bf R}_{1} \)、\({}^{1}{\bf p}_{2} \)、ステップ1で求めた\({}^{0}{\bf R}_{2} \)を用いて以下のように求めます。
$$
\begin{array}{rcl}
{}^{0}{\bf \dot p}_{2} &=& {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf p}_{2} + {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2}
\end{array}
$$
$$ \begin{array}{rcl}
{}^{0}\dot{\bf R}_{2} &=& {}^{0}{\omega}_{1} \times {}^{0}{\bf R}_{2}
\end{array}
$$
ステップ3. (出力2) 基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の位置・姿勢の加速度\( {}^{0}\ddot{\bf p}_{2} \)、\( {}^{0}\ddot{\bf R}_{2} \)
基準座標系\( \Sigma_{0} \)から見た座標系\( \Sigma_{2} \)の位置・姿勢の加速度\( {}^{0}\ddot{\bf p}_{2} \)、\( {}^{0}\ddot{\bf R}_{2} \)を、入力\( {}^{0}{\bf R}_{1} \)、\({}^{1}{\bf p}_{2} \)、\( {}^{1}\ddot{\bf p}_{2} \)、\({}^{0}{\bf \omega}_{1} \)、\({}^{0}{\bf \dot \omega}_{1} \)、ステップ1.で求めた\\( {}^{0}{\bf R}_{2} \)により、以下のように求めます。
$$ \begin{array}{rcl}
{}^{0}\ddot{\bf p}_{2} &=& \
{}^{0}{\bf \dot \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf p}_{2} \
+ {}^{0}{\bf \omega}_{1} \times \left( {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf p}_{2} \right) \
+ 2 {}^{0}{\bf \omega}_{1} \times {}^{0}{\bf R}_{1} {}^{1}{\bf \dot p}_{2} \
+ {}^{0}{\bf R}_{1} {}^{1}{\bf \ddot p}_{2} \\
\end{array}
$$
$$ \begin{array}{rcl}
{}^{0}\ddot{\bf R}_{2} &=& {}^{0}{\dot \omega}_{1} \times {}^{0}{\bf R}_{2} + \
{}^{0}{\omega}_{1} \times \left( {}^{0}{\omega}_{1} \times {}^{0}{\bf R}_{2} \right) \\
\end{array}
$$
6. コリオリの力の実用例
コリオリ式質量流量計
流量計といえば、自分が大学工学部1年で最初に習ったのは、
歯車式、ブローディ(BLODIE)式、ルーツ(ROOTS)式、ドラム式、オーバル式といった容量流量計、
オリフィス・ノズル、ベンチュリ管といった差圧式流量計などでしたが、
コリオリの力を利用したコリオリ式質量流量計というものもあるそうです。
曲がった(部分的に回転カーブした)管の中を通る流量が振動することでコリオリの力を発生させ、2点間の振動の変化をとり質量流量を測定するといった仕組みだそうです。
振動型ジャイロ
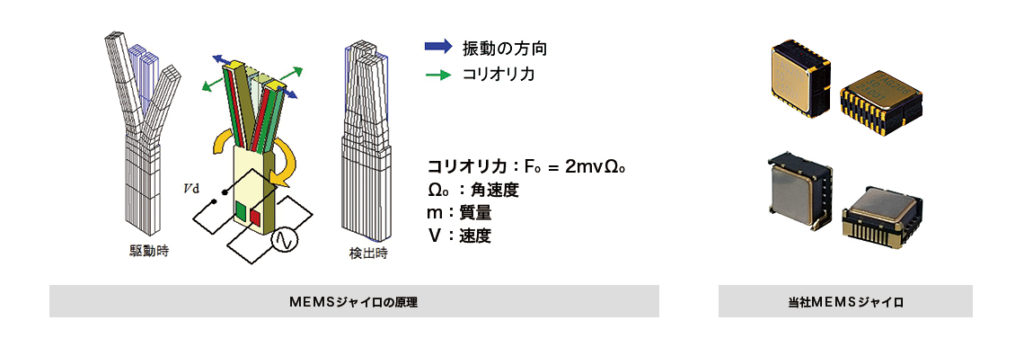
回転角速度を計測するジャイロセンサで、回転体上の振動に加わるコリオリの力を利用して回転角速度を測定する振動型ジャイロスコープという計測器があるそうです。
以下の図のように、多摩川精機さんのMEMSセンサには、
「速度を持った質量に角速度が加わると、速度方向と回転軸の両方に直交する方向にコリオリ力が生じる」という原理を使用して回転角速度を測定されているそうです。
ふぅ~
コリオリの力というと、
長い振り子の先につけた質量の大きいおもりに働くコリオリの力を観測することでレオン・フーコーさんが地球の自転を証明した話とか、
低気圧の移動がコリオリの力を受けて右回りの渦になる、などスケールの大きな話が例に上がるのですが、
もっと工学寄りで身近なセンサにも使われていることに目を向けたいと思い計測器での利用例を探して挙げました。
回転と伸縮が組み合わさった運動をする物体はすべてコリオリの力を受けます。
台座(または腰軸)が高速回転する回転系上で、手先の物体を高速並進移動させるなど、
ロボットの動力学でも、制御モデルの中にコリオリの力を考えておく必要があるでしょう。
以上です。