こんにちは、だいCです。
剛体の運動について、回転に関する話ばかり書いています。
剛体の運動方向の自由度は、「位置」と「姿勢」の2種類で表現してます。
回転方向の自由度を「姿勢」と呼んでいます。
この「姿勢」という言葉は英語だとorientationですかね。
ロボットの全関節角セットで定まる格好を「姿勢」ということもあります。
こちらは英語だとposeですかね。
ややこしいですね。
今回は、姿勢のオフセットについてノートしていきます。
いきなり姿勢のオフセットといわれても話が見えないので、まず目的を述べる前に、例となるお話を先に書きます。
1. 姿勢のオフセットを考える場面
普通売られているマニピュレータには、操作ソフトも付属しており、
ユーザは手先の位置・姿勢を直交座標空間で操作することができます。
内部では、コントローラが手先位置姿勢から各関節指令角へ自動で変換して動かしてくれます。
ユーザは、手先の運動だけ見て動かせるのです。
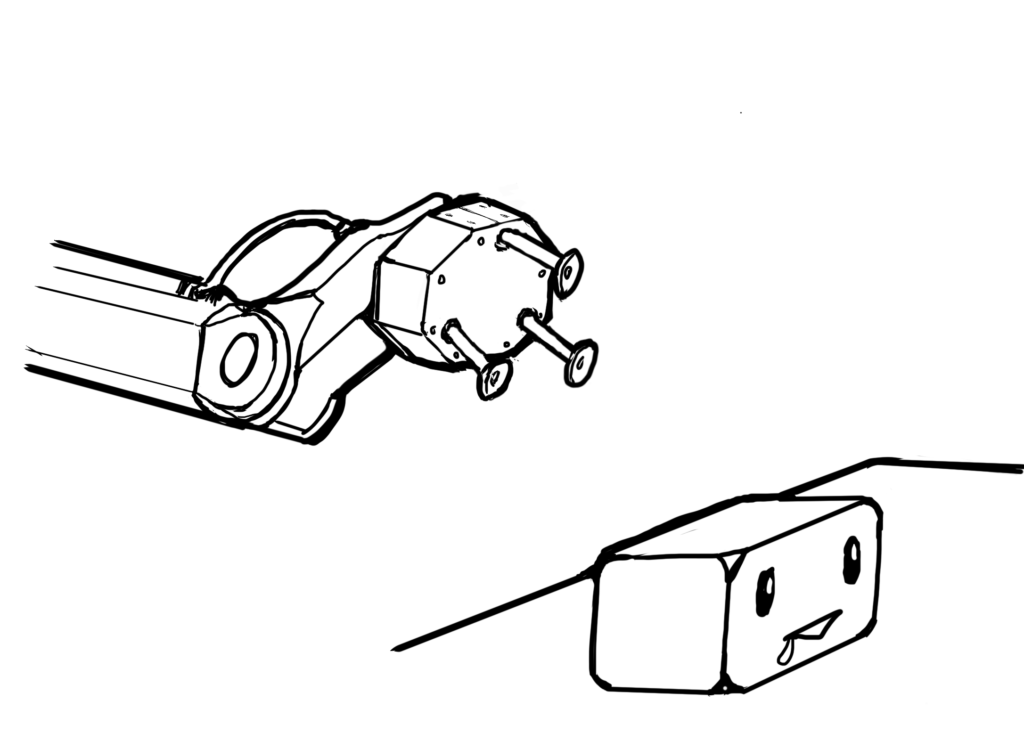
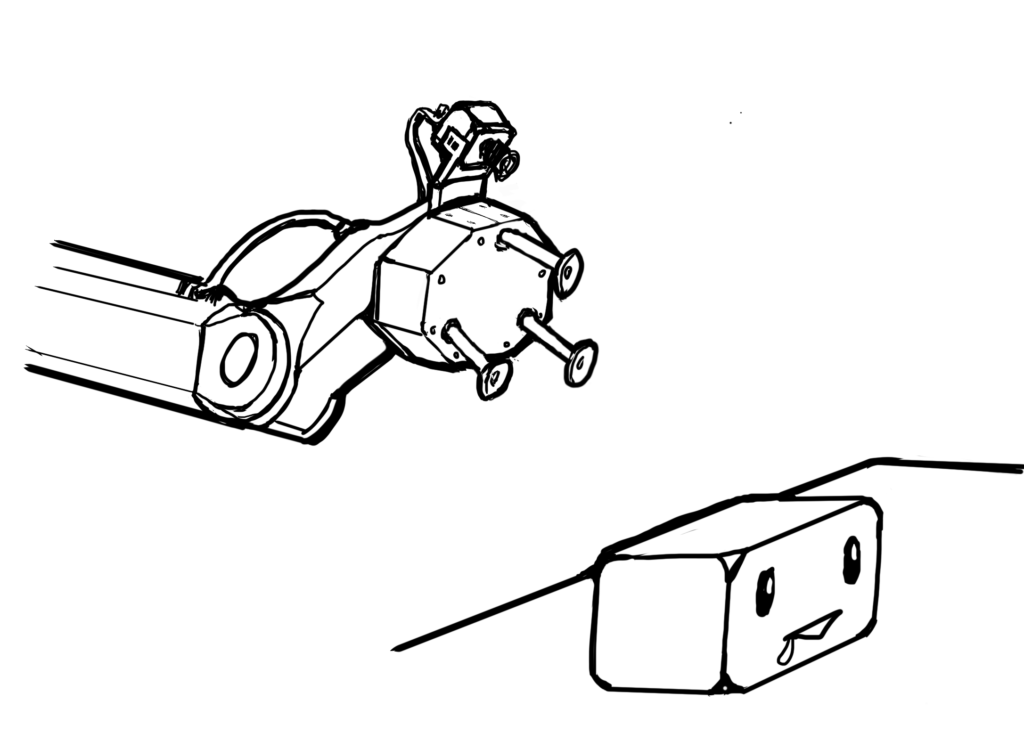
イメージとして、下のようなマニピュレータの手先に吸着ハンドが付いている絵を描いてみました。
(3本飛び出してる棒に吸盤みたいなものが付いててそこから吸引するよーな、そんなイメージで描いた絵です。。伝わりにくかったらゴメンナサイ)
マニピュレータの前には、ハンドで把持する物体が置かれています。
(よだれ垂らした直方体みたいなやつがそれです。。)
ユーザは、この手先についた吸着パッドをうまく物体の面に押し当てて、どっか後ろにつながったポンプの空気圧から生じた吸引力により、物体を吸引して掴み取ろうとしています。
ユーザが、手元にコントローラのようなものを持って、直接ジョグ操作(ボタンを押している間ずっと微量ずつ動かせるような操作、ジョギング操作ともいう)をする場合も考えられます。
そうではなく、ここでは、ロボットがビジョンセンサ等を利用し、物体を自動で認識し、自動で物体をつかむことができるソフトが用意されているとします。
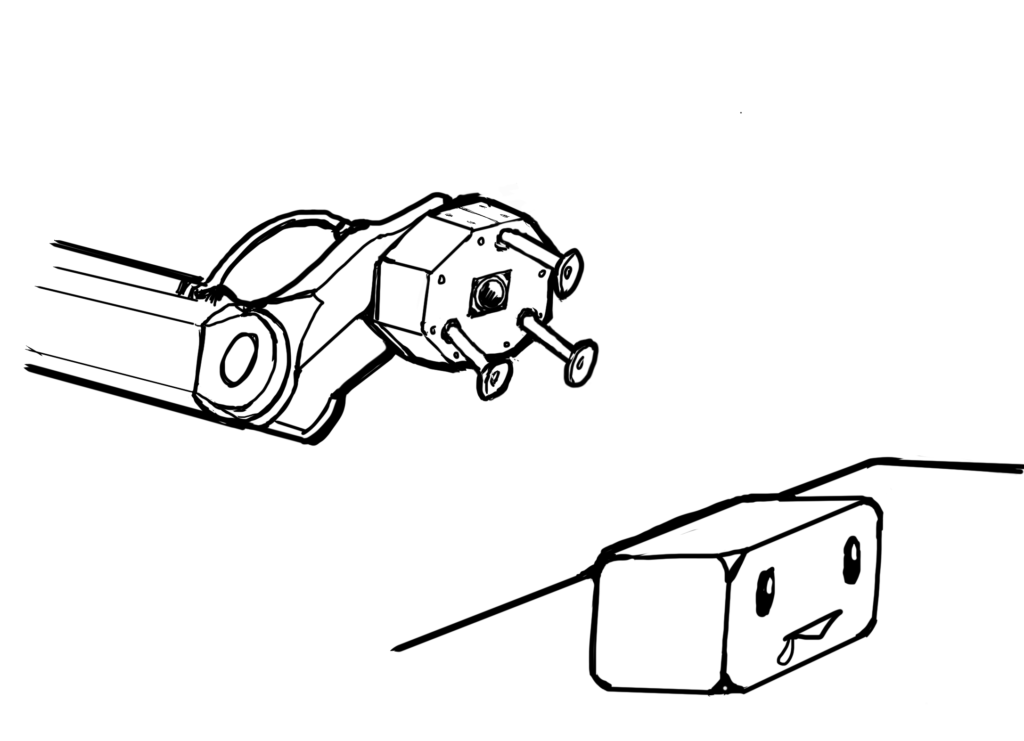
下の絵のように、吸着ハンドにビジョンセンサが取り付けられているとします。
(ハンドの真ん中に描き足したのが、ビジョンセンサ(カメラ・レンズのイメージ)のつもりです。。妄想なのでテキトーです)
ビジョンセンサで撮像した物体の映像から、ビジョンの認識技術により物体の位置姿勢を3次元認識できるとします。
(さらっと仮定しましたが、これだけでコンピュータビジョン(画像処理と認識)の難しいお話が出てきます。本題から逸れるので省略します。)
ビジョンソフトは、ロボットのソフトとは別途用意したとします。
ビジョンでは普通、物体の3次元認識の結果を、センサの座標系基準で得られます。
(カメラだと本体内の、レンズ~受光センサ~基板のどこかの位置に仮想的に置かれた座標系です。焦点距離やレンズの歪補正などによって変わりますが、ここではその座標系が予め設定されているものとします)。
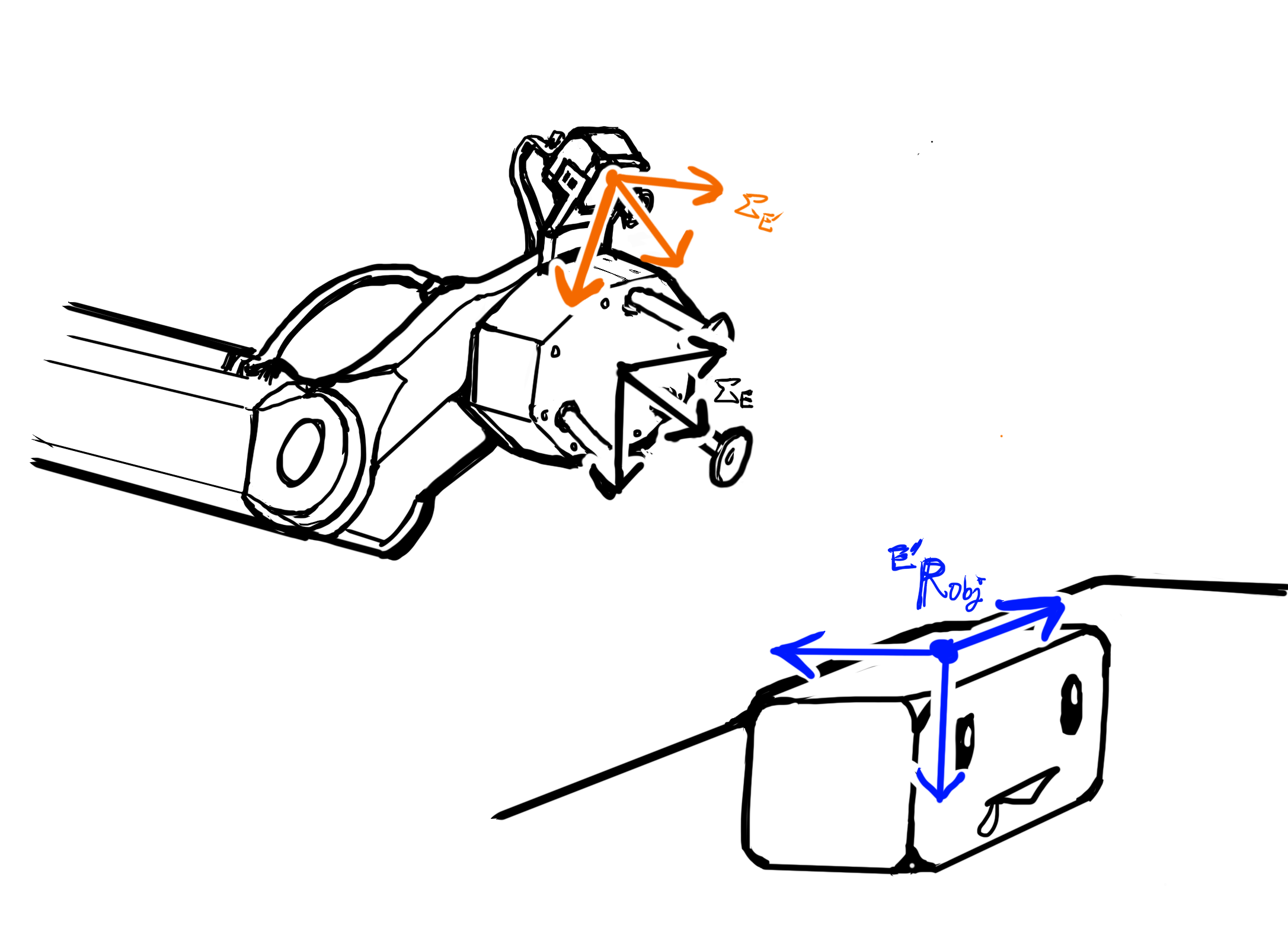
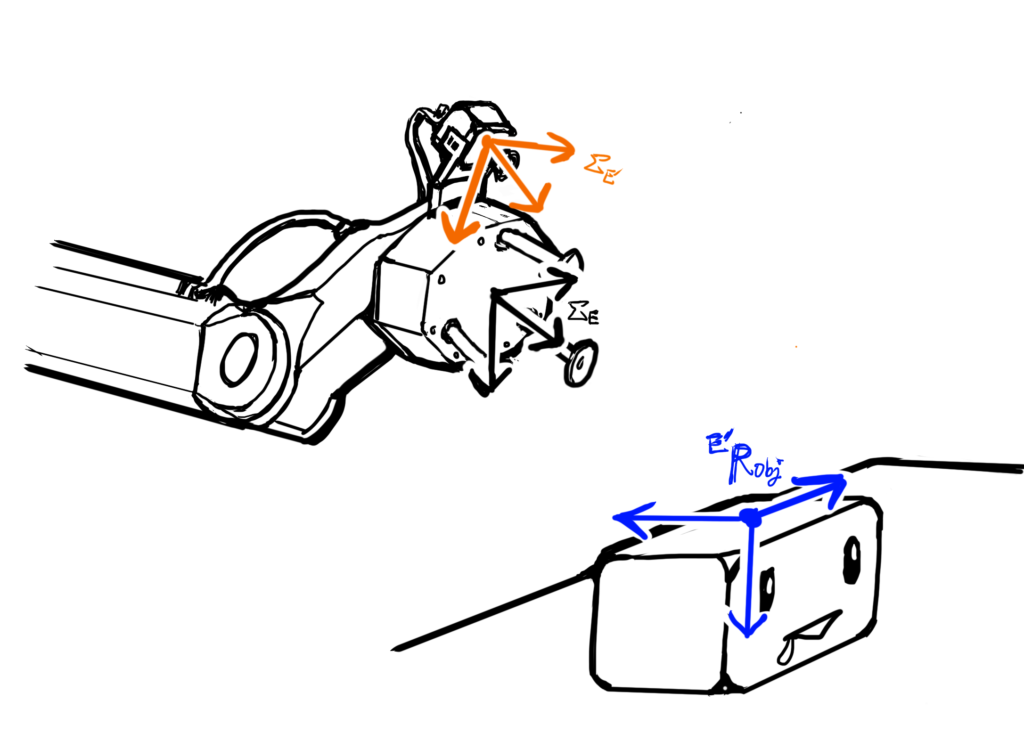
ここで、ロボットの手先位置姿勢に対応する座標系を\( \Sigma_{E} \)とします(黒線で描いた座標系)。
ビジョンセンサの座標系を\( \Sigma_{E’} \)とします(オレンジ線で描いた座標系)。
(下付き文字のラベルEは手先=エンドエフェクタEndEffectorを省略してるつもりです。ビジョンセンサを表したラベルE’も、手先の目のようなものだからEyeでもいいですし、ツールToolのTとする場合もありますね。カメラだからCとかでも。もう何でもいいですラベルの対応さえとれれば)
手先とビジョンセンサの座標系が一体化されていて、
両者の座標系が一致するように設計されているイメージを下の絵のように描いてみました。
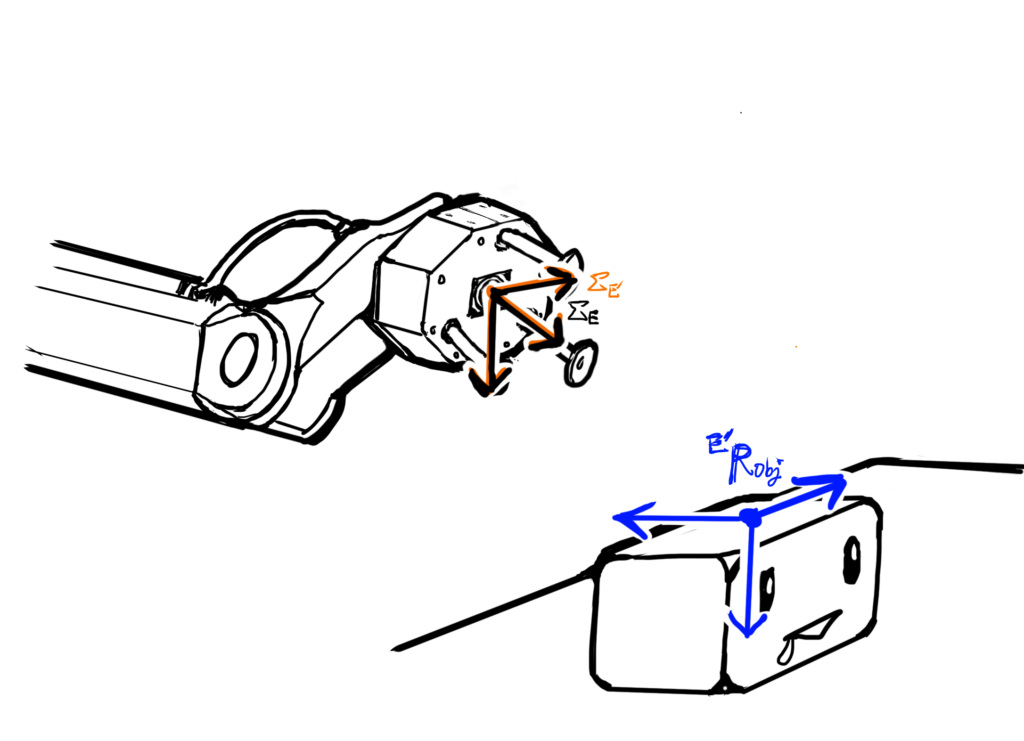
ビジョンセンサから認識された物体の位置姿勢、
ここでは姿勢だけ考えて、物体の姿勢を\( {}^{E’}{\bf R}_{obj} \)とします(objはobjectを省略したラベル)。
\( {}^{E’}{\bf R}_{obj} \)は、座標系\( \Sigma_{E’} \)基準の物体の姿勢を表しているとします。
ビジョンセンサの座標系からみた物体の姿勢\( {}^{E’}{\bf R}_{obj} \)を、手先座標系からみた姿勢\( {}^{E}{\bf R}_{obj} \)へ変換するとき、以下の式で表されます。
$$
{}^{E}{\bf R}_{obj} = {}^{E}{\bf R}_{E’} {}^{E’}{\bf R}_{obj}
$$
上式の座標系変換のオペレータ\( {}^{E}{\bf R}_{E’} \)は、
手先座標系\( \Sigma_{E} \)からみたビジョンセンサ座標系\( \Sigma_{E”} \)の位置姿勢でもあります。
上の絵では、両座標系が一致するよう設計されているので、
$$
{}^{E}{\bf R}_{E’} = {\bf I}
$$
( \( {\bf I} \)は単位行列 )
となります。ビジョンセンサ座標系からみた物体の姿勢は、そのまま手先座標系からみた姿勢になっているわけです。
次に、
手先座標系とカメラ座標系の姿勢が一致せず、
下の絵のように、ハンドとは別に、外付けでビジョンセンサ(カメラ)が付いているケースを考えます。
こちらが今回のメインのお話です。
手先座標系\( \Sigma_{E} \)とビジョンセンサ座標系\( \Sigma_{E”} \)は、下の絵のように姿勢が異なります。
このように姿勢が異なる場合、物体の位置姿勢に合わせて手先を動かそうとすると、
手先座標系\( \Sigma_{E} \)から見たビジョンセンサの座標系\( \Sigma_{E’} \)の位置姿勢、お題の「姿勢のオフセット」を知る必要があります。
「姿勢のオフセット」と述べてますが、姿勢のずれとか、姿勢の誤差とか、姿勢の一定寸法とか、そんな風に解釈してもらっても構いません。JIS用語だと自分が言う手先とはメカニカルインタフェースのことですね(ラベルではエンドエフェクタにしちゃったけど)。姿勢オフセットはJIS用語だと何でしょう。メーカー定義な感じですかね。
2. 目的
姿勢のオフセット\( {}^{E}{\bf R}_{E’} \)を求める。
3. 姿勢のオフセット
以降、ハンドやビジョンセンサや物体について、全て姿勢だけで考えます。
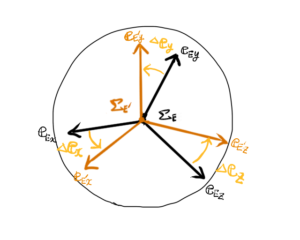
手先座標系とビジョンセンサ座標系の姿勢が一致している図を描きました。
例のごとく、正規直交基底ベクトル\( {\bf e}_{x} \), \( {\bf e}_{y} \), \( {\bf e}_{z} \)とそれらの先が表面に収まる半径1の球を描いています。
黒い線で描いた座標系が手先座標系\( \Sigma_{E} \)で、
オレンジ色の線で描いたものがビジョンセンサ座標系\( \Sigma_{E’} \)です。
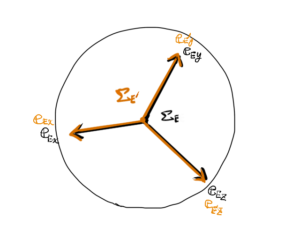
以下のように物体の姿勢\( {}^{E’}{\bf R}_{obj} \)を描きました。
手先座標系から見る物体の姿勢も、ビジョンセンサから見る物体の姿勢も同じです。
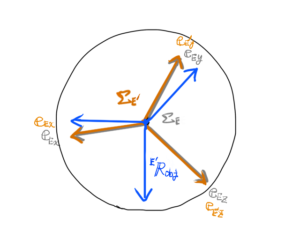
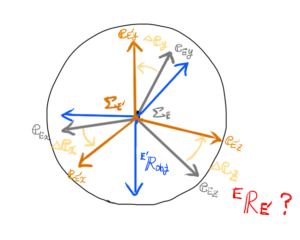
次に本題の、手先座標系とビジョンセンサの座標系の姿勢がずれているときを図に描きます。
さらに物体の姿勢\( {}^{E}{\bf R}_{obj} \)を描きます。
先にも述べましたが、姿勢オフセット\( {}^{E}{\bf R}_{E’} \)は、座標系の相対関係\( \Sigma_{E} \)→\( \Sigma_{E’} \)の座標系変換のオペレータでもあります。
この姿勢オフセット\( {}^{E}{\bf R}_{E’} \)を求める方法を考えてみましょう。
手先座標系\( \Sigma_{E} \)基準で手先をある地点1から地点2に回転移動、もしくは物体を同じ移動量だけ回転したとします。
手先の回転でも物体の回転でも、手先座標系\( \Sigma_{E} \)基準でみると同じ運動として扱えます。
手先の回転運動により、相対的に移動したように見える物体の回転運動も、
手先は移動せず、同じ移動量だけ実際に物体が回転したときの物体の回転運動も
手先座標系\( \Sigma_{E} \)原点から見ると相対的に両方同じになるからです。
(月も太陽も地球から見ると地球のまわりを回って見える現象)
手先座標系\( \Sigma_{E} \)基準で、地点1から2への手先が移動する回転運動オペレータを\( {}^{E}{\bf R}_{obj1 \rightarrow obj2} \)と記述することにします。
地点1の手先座標系\( \Sigma_{E} \)から見た物体の姿勢\( {}^{E}{\bf R}_{obj1} \)、地点2の手先座標系から見た物体の姿勢\( {}^{E}{\bf R}_{obj2} \)により、以下の関係式で表されます。
$$
{}^{E}{\bf R}_{obj2} = {}^{E}{\bf R}_{obj1 \rightarrow obj2} {}^{E}{\bf R}_{obj1}
$$
よって、回転運動のオペレータは、以下のように求まります。
$$
{}^{E}{\bf R}_{obj1 \rightarrow obj2} = {}^{E}{\bf R}_{obj2} {}^{E}{\bf R}_{obj1}^{\rm T}
$$
これが地点1から地点2への手先の回転運動を表しています。
同様にして、ビジョンセンサ座標系\( \Sigma_{E’} \)からみた物体の相対的な移動量は、
回転運動のオペレータ\( {}^{E’}{\bf R}_{obj1 \rightarrow obj2} \)により以下のよう書き表すことができます。
$$
{}^{E’}{\bf R}_{obj1 \rightarrow obj2} := {}^{E’}{\bf R}_{obj2} {}^{E’}{\bf R}_{obj1}^{\rm T}
$$
では、
このビジョンセンサ座標系\( \Sigma_{E’} \)基準の物体の地点1から地点2への回転運動を、
手先座標系基準\( \Sigma_{E} \)基準に座標系変換してみようと思います。
回転運動に座標系変換のオペレータ\( {}^{E}{\bf R}_{E’} \)をかけます。
$$ \begin{array}{rcl}
{}^{E}{\bf R}_{E’} \left( {}^{E’}{\bf R}_{obj2} {}^{E’}{\bf R}_{obj1}^{\rm T} \right)
&=& {}^{E}{\bf R}_{E’} \left(
{}^{E’}{\bf R}_{E} {}^{E}{\bf R}_{obj2} \left(
{}^{E’}{\bf R}_{E} {}^{E}{\bf R}_{obj1} \right)^{\rm T}
\right) \\
&=& {}^{E}{\bf R}_{obj2} {}^{E}{\bf R}_{obj1}^{\rm T} {}^{E}{\bf R}_{E’} \\
&=& {}^{E}{\bf R}_{obj1 \rightarrow obj2} {}^{E}{\bf R}_{E’}
\end{array}
$$
最終的に以下の式が導けます。
$$
{}^{E}{\bf R}_{E’} \left( {}^{E’}{\bf R}_{obj2} {}^{E’}{\bf R}_{obj1}^{\rm T} \right)
= {}^{E}{\bf R}_{obj1 \rightarrow obj2} {}^{E}{\bf R}_{E’}
$$
上の式が表す意味は以下のようになります。
$$ \begin{array}{lcl}
{}^{E}{\bf R}_{E’}^{\rm T}
\left( ({\rm ビジョンセンサからみた地点2の物体姿勢}) ( {\rm ビジョンセンサからみた地点1の物体姿勢} )^{\rm T} \right)
&& \\
\ \ \ \ = ({\rm 手先座標系からみた地点1 \rightarrow 2の手先回転運動})
{}^{E}{\bf R}_{E’}
& &
\end{array} $$
式中に日本語で書いた
- ビジョンセンサからみた地点1の物体姿勢
- ビジョンセンサからみた地点2の物体姿勢
- 手先座標系からみた地点1\( \rightarrow \)2の手先回転運動
は、ビジョンの認識機能、ロボットの手先運動制御機能によりそれぞれ計測・取得できるとします。
なので既知の定数として、
1.,2.のビジョン認識機能より計測される\({}^{E’}{\bf R}_{obj2} {}^{E’}{\bf R}_{obj1}^{\rm T} \)の3×3行列を\( {\bf A} \)、
3.のロボットの手先運動制御機能により取得される\( {}^{E}{\bf R}_{obj1 \rightarrow obj2} \)の3×3行列を\( {\bf B} \)、
知りたい姿勢オフセットの3×3行列\( {}^{E}{\bf R}_{E’} \)を\( \bf X \)とおけば、
式は、
$$
{\bf X} {\bf A} = {\bf B} {\bf X}
$$
の形の行列方程式になることがわかります。
あとは、この行列\( \bf X \)を求めて姿勢オフセット\( {}^{E}{\bf R}_{E’} \)を得ることができます。
ここでは、行列方程式解法の詳細は省略します。
ふぅ~、、
落書きみたいな図をいっぱい描いちゃいました。。
この話は、カメラから手先の姿勢オフセットだけでなく、
手先からさらに伸びた上記吸着パッドとか爪とかチャックとかの、ツール先端(TCP:Tool Center Pointと呼ばれる点)の姿勢オフセットを考える時にも有効です。
ただしその場合は、上記ビジョンによる計測だけではなく、ツール先端を計測器具で物理的に計測したり、またはマニピュレータを決まった回転軸と回転角だけ移動させるなど別途拘束条件を設けたりして求めてもいいと思います。
姿勢オフセットの話は、マニピュレータ使用上よく出るのですが、あまりロボット工学の教科書には書かれてませんね。
簡単なようでややこしいです。
物理世界の話をしているけど、仮想的な設定が多いんで、これなんだっけ??ってなっちゃいます。
一度自分の中で消化するまで整理した方がいいですね。
今回は、Dr.の同僚に教えてもらったりして書かせてもらいました。感謝!
まだまだ回転の話は続きますが、、
今回は以上です。